Data Structure questions for Computer Science and MCA students

Write short note on ADT.

What is ADT?

ADT stands for Abstract Data Type.
It is a mathematical model of a data structure.
ADT describes a container which holds a finite number of objects where the objects may be associated through a given binary relationship.
It is a logical description of how we view the data and the operations that are allowed without regard to how they will be implemented.
It concerns only with what the data is representing and not with how it will eventually be constructed.
It is a set of objects and operations, for example: list, insert, delete, serach, sort.

Abstract Data Types (ADTs)

Following are the some basic ADTs of data structure:
Stack
Queue
Linked List

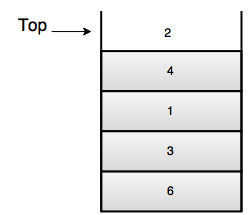
1. Stack

It is a list where insert and remove take place only at the top.
It performs LIFO(Last In First Out) operation.

Operations of Stack
Push: Insert element on top of stack.
Pop: Remove element from top of stack.
Top: Return element at top of stack.
stack

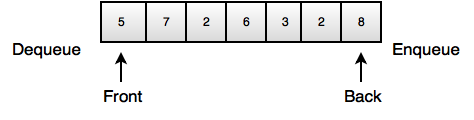
2. Queue

It is a list where insert takes place at the back, but remove takes place at the front.
It performs FIFO(First In First Out) operation.

Operations of Queue

Enqueue: Insert element at the back of the queue.
Dequeue: Remove and return element from the front of the queue.
queue

3. Linked List

It is a linear collection of data elements, called nodes pointing to the next node by means of pointer.
Each node consists of its own data and the address of the next node and forms and chain.
It is used to create trees and graphs.

Advantages of ADT

It is reusable and ensures robust data structure.
It can be re-used at several places.
It reduces coding efforts.
Encapsulation ensures that data cannot be corrupted.
It is based on principles of Object Oriented Programming (OOP) and Software Engineering (SE).

Explain space and time complexity.

Time Complexity: It is the amount of time an algorithm takes in terms of the amount of input data to algorithm. It is calculated on the basis of different criteria such as:

The number of times the memory is being accessed.
The number of comparisons between variables.
The number of time loops is executed etc.

Space Complexity: It is the amount of memory an algorithm takes in terms of the amount of input data to the program. If an algorithm takes less time to execute and takes less memory, then it is considered as best algorithm.

Example:
The running time of a loop is, at most, the running time of the statements inside the loopmultiplied by the number of iterations.

for (i=1; i<=n; i++)
{
m = m + 2; //constant time, c
}
Total time = a constant c * n = cn = 0(n)

Find the time complexity of given below code. Ignore syntax error.

Fun()
{
     Inti = 1, s = 1;
     while(s<=n)
     {
          i++;
          s = s + i;
          printf(“CareerRide”);
     }
}

Solution:
Let us see how the value of s is change with respect to i. The loop will stop when the condition s<=n.

I =	1	2	3	4	5	6
S =	1	3	6	10	15	21

Suppose that it will stop after k iteration. Means the condition s<=n met after k iteration. The value of s is summation of i.

k(k+1)/2 > n
k2 + k > 2n
k = O (n1/2)

Output
Time complexity = O (n^1/2)

Find the time complexity of given below code. Ignore syntax error.

Fun()
{
     int i, j, k, n;
     for (i=1; i<=n; i++)
     {
          for (j=1; j<=i; j++)
          {
               for (k=1; k<=100; k++)
               {
                    Printf(“CareerRide”);
               }
          }
     }
}

Solution:

If i =	1	2	3	4	5		n
Then inner loop will execute j<=i	1 time	2 time	3 time	4 time	5 time	.... and so on	n time
Most inner loop will execute K<=100	100 times	200 times	300 times	400 times	500 times		n * 100 times

So the total time will be

= 100 + 2 * 100 + 3 * 100 + 4 * 100....n * 100
= 100 (1 + 2 + 3 + 4………n)
= 100 [n(n + 1)/2]
= 100 [(n² + n)/2]
= O (n²)

Output
Time complexity = O (n²)

Find the time complexity of given below code. Ignore syntax error.

A()
{
     for(i = 1; i<n; i = i * 2)
     {
          Printf(“careerRide”);
     }
}

Solution:
Initial value of i is 1 and it is incremented by the expression i = i * 2.

I =	1	2	4	8	16	32
i = i * 2	2	4	8	16	32	64

So the series will be as follows.
2⁰, 2¹, 2², 2³, 2⁴, 2⁵, .......,

Let us assume after k iteration loop will stop, so

2^k = n
K = log₂n

Output
Time complexity = O (Log₂n)

Find the time complexity of given below code. Ignore syntax error.

A()
{
     for(i=n/2; i<=n; i++)
     {
          for(j=1; j<=n/2; j++)
          {
               for(k=1; k*lt;=n; k=k*2)
               {
                    Printf(“CareerRide”);
               }
          }
     }
}

Solution:
The first loop will execute n/2 times, second loop will also execute n/2 times. According to above question the time complexity of last loop will be log₂n.
So the time complexity will be = n/2 * n2 * log₂n.
= n²log₂n.

Output
Time complexity = O (n²log₂n)

Data Structure questions for Computer Science and MCA students

Write short note on ADT.

Explain space and time complexity.

Find the time complexity of given below code. Ignore syntax error.

Find the time complexity of given below code. Ignore syntax error.

Find the time complexity of given below code. Ignore syntax error.

Find the time complexity of given below code. Ignore syntax error.

Related Content