Problems on H.C.F and L.C.M - Aptitude test, questions, shortcuts, solved example videos

  • Online aptitude test >> Problems on H.C.F and L.C.M - Aptitude test, questions, shortcuts, solved example videos
Video on Problems on H.C.F and L.C.M - shortcuts, tips and tricks

H.C.F and L.C.M of numbers

Why is H.C.F and L.C.M important?
The chapter of H.C.F and L.C.M is very important. This concept is useful in the chapters of time and distance, time and work, pipes and cisterns, etc. The tricks used to find
L.C.M and H.C.F of two or more numbers help in finding out quick solutions and thus reduce time during exams.

L.C.M. concept is important to solve problems related to racetracks, traffic lights, etc.
H.C.F. concept is useful in calculating the largest size of tile/room in particular area, largest tape to measure the land, etc.

Important terms:

1) Factors: Factor is a number which exactly divides other number.
Example: 3 and 5 are factors of 15

2) Multiple: A number is said to be multiple of another number, when it is exactly divisible by other number.
Example: 15 is a multiple of 3 and 5

3) Common multiple: A common multiple of two or more numbers is a number which is exactly divisible by each of them.
Example: 18 is a common multiple of 2,3,6 and 9

4) H.C.F/G.C.F: (Highest Common Factor / Greatest Common Factor). H.C.F of two or more numbers is the greatest number which divides each number exactly.

5) L.C.M.: (Lowest common multiple). The least number exactly divisible by each one of the given numbers is called least common multiple.

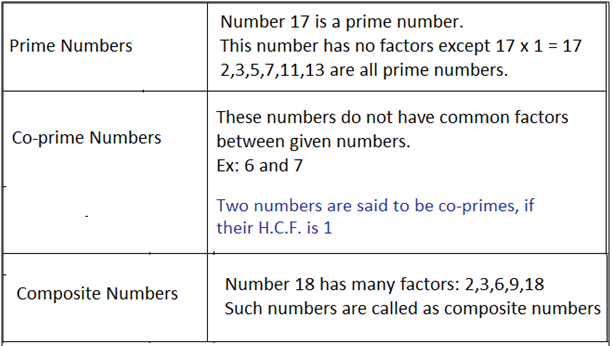
Points To Remember:

1) Before studying this chapter, make sure that the basic concepts of numbers (prime numbers, composite numbers, co-prime numbers, etc) are perfectly understood. Knowing basics will help in understanding this chapter.

Quick Revision of prime numbers, composite numbers and co-prime numbers is given below:



2) (H.C.F)
a) It is the greatest number which exactly divides all the given numbers.
b) The H.C.F of two or more numbers is smaller than or equal to the smallest number of given numbers.
c) H.C.F of given numbers divides their L.C.M.
d) Two numbers are said to be co-prime if their H.C.F. is 1.

3) (L.C.M)
a) To find L.C.M. of two co-prime numbers, just multiply the given two numbers.
b) The L.C.M. of two or more numbers is greater than or equal to greatest number of given numbers.

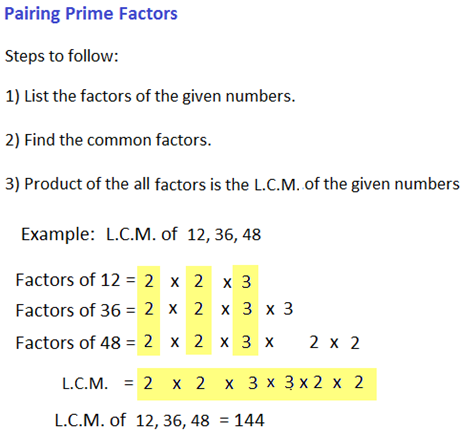
Methods to Find H.C.F. of Given Numbers







Methods to Find L.C.M. of Given Numbers







Tips and Tricks:

1) H.C.F. and L.C.M. of Fractions
a) H.C.F. = H.C.F. of Numerator
L.C.M. of Denominator

Example
H.C.F. of l, m, n = H.C.F. of (l, m, n)
abcL.C.M. of (a, b, c)

b) L.C.M. = L.C.M. of Numerator
H.C.F. of Denominator

L.C.M. of l, m, n = L.C.M. of (l, m, n)
abcH.C.F. of (a, b, c)

2) Product of two numbers = Product of their H.C.F. and L.C.M.
This condition is only true for two given numbers. If H.C.F. and L.C.M. of three or more numbers are given, then this rule is not applicable.

3) H.C.F. and L.C.M. of decimal fractions: To find H.C.F. or L.C.M. of 0.5, 1.6, etc, consider these numbers without decimal point i.e 5, 16 and solve using normal methods used to determine H.C.F. or L.C.M.. In the result, mark off as many decimal places as there are in each of the given number.

4) Comparison of fractions: Find L.C.M. of denominators of given fractions. Convert each fraction into equivalent fraction with L.C.M. as denominator, by multiplying both numerator and denominator by same number. The resultant fraction with the greatest numerator is greatest.

Question Variety:

Generally 5 types of questions are asked in this chapter. Understanding and studying these concepts will in solving this chapter as well as help in solving some topics in other chapters.

Type 1: Find H.C.F. and L.C.M of composite numbers


Q 1. H.C.F. of 513, 1134 and 1215 is _____________

a. 18
b. 27
c. 33
d. 36
View solution

Correct Option: (b)

We know different methods to calculate H.C.F.
Finding H.C.F. by division method:



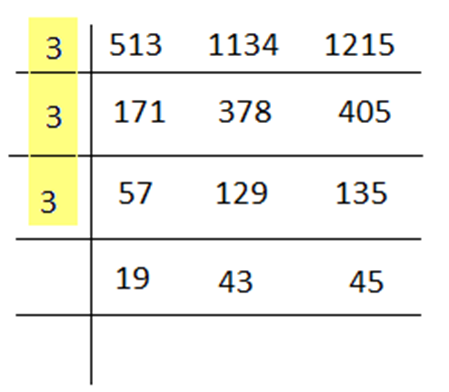
H.C.F. of 513, 1134 and 1215 = 3 × 3 × 3 = 27


Q 2. Find the least number which is exactly divisible by 12, 15, and 20.

a. 40
b. 50
c. 60
d. 80
View solution

Correct Option: (c)

Remember: The question may be asked in a tricky way.
Least number = L.C.M. of 12, 15, and 20. We have to find the least number.



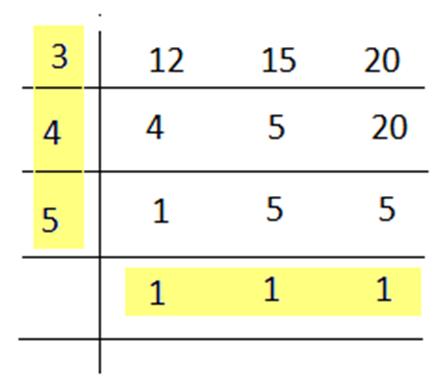
In this case, 20 is not divisible by 3, hence, write down as it is. 20 is further divisible by 4.
L.C.M. = 3 × 4 × 5 × 1 × 1 × 1 = 60
Hence, the required least number = 60


Q 3. Find the largest number of 4-digits divisible by 12, 15 and 18.

a. 9900
b. 9750
c. 9450
d. 9000
View solution

Correct Option: (a)

Largest 4-digit number is 9999.
Remember: The question may be asked in a tricky way. Here, largest number does not mean H.C.F.. We have to find a number which is divisible by 12, 15 and 18
Required largest number must be divisible by the L.C.M. of 12, 15 and 18
L.C.M. of 12, 15 and 18
12 = 2 × 2 × 3
15 =5 × 3
18 = 2 × 3 × 3
L.C.M. = 180
Now divide 9999 by 180, we get remainder as 99
The required largest number = (9999 – 99) =9900
Number 9900 is exactly divisible by 180.

Type 2: Find H.C.F. and L.C.M. of decimal numbers and fractions


Q 4. Find H.C.F. of 0.63 and 1.05

a. 0.21
b. 0.28
c. 0.56
d. 0.84
View solution

Correct Option: (a)

Hint: If numbers are in decimal form, convert them without decimal places. Therefore, the numbers are 63 and 105.



H.C.F. of 63 and 105 is 21.
In decimal form: H.C.F. = 0.21


Q 5. Find L.C.M. of 1.05 and 2.1

a. 1.3
b. 1.25
c. 2.1
d. 4.30
View solution

Correct Option: (c)

Hint: If numbers are in decimal form, convert them without decimal places. Therefore, the numbers are 105 and 210.



L.C.M. = 5 x 7 x 3 x 2 = 210
L.C.M. of 105 and 210 = 210
In decimal form: L.C.M. = 2.1

Q 6. Calculate H.C.F. of 2, 16, 8
3819

a. 2
9
b. 8
3
c. 2
81
d. 3
16
View solution

Correct Option: (c)

Hint:

H.C.F. = H.C.F. of Numerator
L.C.M. of Denominator
H.C.F. = H.C.F. of 2, 16, 8
L.C.M. of 3, 81, 9

H.C.F. of 2, 16, 8
2 = 21
8 = 23
16 = 24
Number with least index = 21 = 2
H.C.F. of 2, 16, 8 = 2

L.C.M. of 3, 81, 9
3 = 31
9 = 32
81 = 34
Number with highest index = 34 = 81
L.C.M. of 3, 81, 9 = 81
H.C.F. = 2
81

Q 7. Find L.C.M. of 2, 8, 64, 10
398127

a. 250
9
b. 160
3
c. 128
9
d. 320
3
View solution

Correct Option: (d)

Hint:

L.C.M. = L.C.M. of Numerator
H.C.F. of Denominator
L.C.M. of numerators = 2, 8, 64, 10
2 = 21
8 = 23
64 = 26
10 = 2 × 5
L.C.M of 2, 8, 64, 10 = 26 × 5 = 320

H.C.F. of denominators = 3, 9, 81, 27
3 = 31
9 = 32
81 = 34
27 = 33
H.C.F. of 3, 9, 81, 27 = 3
L.C.M. of2, 8, 64, 10 = 320
3981273

Type 3: Find the numbers/sum of numbers/product of numbers if
1) Their ratio and H.C.F. are given.
2) Product of H.C.F. and L.C.M are given.


Q 8. H.C.F. of two numbers is 13. If these two numbers are in the ratio of 15: 11, then find the numbers.

a. 230, 140
b. 215, 130
c. 195, 143
d. 155, 115
View solution

Correct Option: (c)

Hint: Product of two numbers = Product of their H.C.F. and L.C.M.
Given:
1) H.C.F. of two numbers = 13
2) The numbers are in the ratio of 15 : 11

Let the two numbers be 15y and 11y
H.C.F. is the product of common factors
Therefore, H.C.F. is y. So y = 13

The two numbers are:
15y = 15 × 13 = 195
11y = 11 × 13 = 143
We can cross-check the answer using the trick. (Product of two numbers = Product of their H.C.F. and L.C.M.)
Product of H.C.F. and L.C.M. = 13 × 2145 = 27885
Product of two numbers = 195 × 143 = 27885
Hence, the calculated answer is correct.


Q 9. If the product and H.C.F. of two numbers are 4107 and 37 respectively, then find the greater number.

a. 111
b. 222
c. 332
d. 452
View solution

Correct Option: (a)

4107 is the square of 37.
So let two numbers be 37x and 37y.
37x × 37y = 4107
xy = 3
3 is the product of (1 and 3)
x = 1 and y = 3
37x = 37 × 1 =37
37y = 37 × 3 = 111
Greater number = 111
OR
Hint:
Product of two numbers = Product of their H.C.F. and L.C.M.
Product of two numbers = 4107
4107 = 37 × L.C.M

L.C.M. = 4107 = 111
37
The greater number = 111


Q 10. Find the sum of two numbers, which are greater than 29 and have H.C.F. and L.C.M. of 29 and 4147 respectively.

a. 858
b. 696
c. 1050
d. 4147
View solution

Correct Option: (b)

Hint:
Product of two numbers = Product of their H.C.F. and L.C.M.
Product of two numbers = 29 × 4147 = 120263
Given: Two numbers are greater than 29.
Therefore, let the two numbers be 29x and 29y.
So, 29x × 29y = 120263
Xy = 143
Factors of 143 are: 1, 11, 13, and 143

Case: 1) If we consider factors of 143 as 1 and 143 (co-primes), then we get the value of two numbers x and y = (29 and 4147) ------ (Which is wrong: As it is given that, the numbers are greater than 29)
Case: 2) If we consider factors of 143 as 11 and 13 (co-primes), then we get the value of two numbers x and y = (319, 377) ------ (These two values are greater than 2. So, it is the correct answer)
Therefore, the two numbers are 319 and 377.
Sum of two numbers = 319 + 377 = 696

Type 4: Find the least number, which when divided by another number leaves a remainder.


Q 11. Find the greatest number, which on dividing 1657 and 2037 leaves remainders 6 and 5 respectively.

a. 127
b. 132
c. 114
d. 108
View solution

Correct Option: (a)

The number on dividing 1657 and 2037 leaves remainders 6 and 5 respectively.
Hence, make the dividend completely divisible by the divisor. This is possible, if we subtract remainder from the dividend.
Therefore,
1657 – 6 = 1651
2037 – 5 = 2032
H.C.F. of 1651 and 2032 is 127. 127 is the common factor.
127 × 13 = 1651
Thus by adding 6, we get 1651 + 6 = 1657
127 is the correct answer.


Q 12. Find the least number, which when divided by 12, 15, 20 and 54 leaves a remainder of 8 in each case.

a. 548
b. 540
c. 532
d. 524
View solution

Correct Option: (a)

We are given that, the least number, when divided by 12, 15, 20 and 54 leaves a remainder of 8 in each case.
Therefore, add remainder 8 to the L.C.M. of divisors.
The required least number = (L.C.M. of 12, 15, 20 and 54) + remainder (8)
L.C.M. of 12, 15, 20 and 54



L.C.M. = 2 × 3 × 2 × 5 × 9 × 1 = 540
The required least number = (540) + (8) = 548


Q 13. Find the least number which when divided by 5, 6, 7 and 8 leaves a remainder 3, but when divided by 9 leaves no remainder.

a. 1963
b. 2523
c. 1683
d. 1536
View solution

Correct Option: (c)

This is truly a logical question and can just be solved using divisibility test.

Given:
The least number when divided by 9 leaves no remainder.
Divide all the given options by 9 and check whether any number leaves no remainder.

Option a)1963 = 218.11
9
Option b)2523 = 280.33
9
Option c)1683 = 187
9
Option d)1536 = 170.66
9
Option c) 1683 is completely divisible by 9. Hence, the least number is 1683

Type 5: Application based numerical of H.C.F. and L.C.M.



Q 14. The traffic lights at three different road crossings change after every 40 sec, 72 sec and 108 sec respectively. If they all change simultaneously at 5 : 20 : 00 hours, then find the time at which they will change simultaneously.

a. 5 : 28 : 00 hrs
b. 5 : 30 : 00 hrs
c. 5 : 38 : 00 hrs
d. 5 : 40 : 00 hrs
View solution

Correct Option: (b)

Traffic lights at three different road crossings change after every 40 sec, 72 sec and 108 sec respectively.
Therefore, find the L.C.M. of 40, 72 and 108.
L.C.M. of 40, 72 and 108 = 1080
The traffic lights will change again after 1080 seconds = 18 min
The next simultaneous change takes place at 5 : 38 : 00 hrs.


Q 15. A rectangular courtyard 4.55 meters long and 5.25 meters wide is paved exactly with square tiles of same size. Find the largest size of the tile used for this purpose?

a. 25 cm
b. 45 cm
c. 21 cm
d. 35 cm
View solution

Correct Option: (d)

Here, we are asked to find the largest size of tile. Therefore, calculate H.C.F.
Step 1: Covert numbers without decimal places i.e 455 cm and 525 cm
Step 2: Find the H.C.F. of 455 and 525
H.C.F. of 455 and 525 = 35 cm
Hence, the largest size of the tile is 35 cm.


Q 16. 5 bells commence tolling together and toll at intervals 2, 4, 6, 8 and 10 seconds respectively. Find in 40 minutes, how many times do they toll together?

a. 8 times
b. 19 times
c. 21 times
d. 30 times
View solution

Correct Option: (c)

Given: 5 bells commence tolling together and toll at intervals 2, 4, 6, 8 and 10 seconds respectively
Hence, find the L.C.M. of 2, 4, 6, 8 and 10 seconds.



L.C.M. of 2, 4, 6, 8 and 10 = 2 × 2 × 2 × 3 × 5 × 1 = 120
Hence, the bells toll together after 120 seconds = 2 min
We are asked to find, how many times they will toll together in 40 min.

In 40 min, they toll together for = 40 + 1 = 21 times
2


Q 17. John, Smith and Kate start at same time, same point and in same direction to run around a circular ground. John completes a round in 250 seconds, Smith in 300 seconds and Kate in 150 seconds. Find after what time will they meet again at the starting point?

a. 30 min
b. 25 min
c. 20 min
d. 15 min
View solution

Correct Option: (b)

L.C.M. of 250, 300 and 150 = 1500 sec
Dividing 1500 by 60 we get 25, which mean 25 minutes.
John, Smith and Kate meet after 25 minutes.


Practice questions on HCF and LCM
Problems on Decimal - Aptitude test, questions, shortcuts, solved example videos
Problems on Decimal - Quantitative aptitude tutorial with easy tricks, tips & short cuts explaining the concepts of the chapter. Online aptitude preparation material with practice question bank, examples, solutions and explanations. Video lectures to prepare quantitative aptitude for placement tests & competitive exams like MBA, Bank exams, RBI, IBPS, SSC, SBI, RRB, Railway, LIC, MAT. Very useful for freshers, engineers & software developers taking entrance exams. Learn and take practice tests!
Problems on Fraction - Aptitude test, questions, shortcuts, solved example videos
Problems on Fraction - Quantitative aptitude tutorial with easy tricks, tips & short cuts explaining the concepts of the chapter. Online aptitude preparation material with practice question bank, examples, solutions and explanations. Video lectures to prepare quantitative aptitude for placement tests & competitive exams like MBA, Bank exams, RBI, IBPS, SSC, SBI, RRB, Railway, LIC, MAT. Very useful for freshers, engineers & software developers taking entrance exams. Learn and take practice tests!
Problems on Simplification - Aptitude test, questions, shortcuts, solved example videos
Problems on Simplification - Quantitative aptitude tutorial with easy tricks, tips & short cuts explaining the concepts. Online aptitude preparation material with practice question bank, examples, solutions and explanations. Video lectures to prepare quantitative aptitude for placement tests & competitive exams like MBA, Bank exams, RBI, IBPS, SSC, SBI, RRB, Railway, LIC, MAT. Very useful for freshers, engineers & software developers taking entrance exams. Learn and take practice tests!
Post your comment
Discussion Board
Quantitative and aptitude
In Hcf and Lcm 1 question the anwser is correct but there is one calculation mistake in it. Instead of 126 it been written as 129.

This is not a big mistake but correcting it will be more fine.
thank you...
BALA HARI VIGNESH. V 03-6-2022
Correction in Answer
The answer to Question 14 is wrong it should be option C
Aditya Negi 03-19-2020
LCM and HCF
amazing post....
Proper explanation, examples, solved questions.....
Goodinfo 12-29-2019
Bells
it is 21 because of 20 +1 where 1 is the time when bells had rung already .
bells have completed ringing once this can be seen from the fact that we are able to count the commence time.
Rm 07-21-2019
Why did you add 1 to the 'bells tolling' question ?
I understood when we divide 40/2 but why did you add 1 to it at the end ?
Rahul 10-14-2018
Aptitude preparation
Hello. Ive been trying to join ur facebook group but i didnt get any approval yet. Kindly add me there and please i have another request that please provide me the material for percentage ratio n proportion age problems hcf n lcm practice questions separately. G
Faizan 05-13-2018
Maths
This is the best way .....
Bhunesh 05-3-2018
Maths
This is the best way .....
Bhunesh 05-3-2018

Related Content

Follow us

▲