Ratio and Proportion - Aptitude test, questions, shortcuts, solved example videos

  • Online aptitude test >> Ratio and Proportion - Aptitude test, questions, shortcuts, solved example videos
Video on Ratio and Proportion - shortcuts, tips and tricks

Ratio and Proportion

Ratio:

- The ratio of two quantities a and b of same units is the fraction x/y, where b ≠ 0

- The fraction x/y can be represented as x:y

Different types of ratios are:

1) Duplicate ratio: It is the ratio of squares of two numbers.
Duplicate ratio of the fraction x is given as: x = x2 or x : y = x2 : y2
yyy2

2) Sub-duplicate ratio: It is the ratio between square roots of two numbers.
Duplicate ratio of the fraction x is given as: x = x or x : y = x : y
yyy

3) Triplicate ratio: It is the ratio of cubes of two numbers.
Triplicate ratio of the fraction x is given as x = x3
yyy3

4) Sub- Triplicate ratio: It is the ratio between cube roots of two numbers
Sub-Triplicate ratio of the fraction x is given as x = x(1/3)
yyy(1/3)

5) Compound ratio: It is the ratio of product of first terms in every ratio to that of product of second term in every ratio.

For example:
Compound ratio of (a : x), (b : y), (c : z) is (abc : xyz)

6) Inverse ratio: The ratio formed by interchanging their old places in the ratio to new

The inverse ratio of 5 : 8 is 8 : 5.

Proportion:

1) Proportion is the equality of two ratios.

When (a : b = x : y) is represented as (a : b :: x : y), then a, b, x, y are said to be in proportion.

In (a : b :: x : y), a and y are called as extremes and b and x are called as mean terms.

Product of means = Product of extremes

2) Mean proportion: Mean proportion between x and y is given as xy

3) Third proportion: If p : q = q : s, then s is called as third proportional to p and q.

4) Fourth proportion: If u : v = x : y, then y is the fourth proportional of u, v and x.

Quick Tips and Tricks

1) Comparison of ratios:
If (x : y) > ( a : b) → x > a
yb

2) Proportion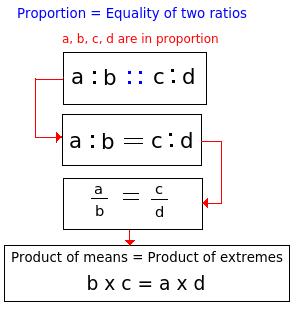


4) Variation:
- If a = kb for some constant k, then we can say that a is directly proportional to b.
- If ba =k for some constant k, then we can say that a is inversely proportional to b.

5) If ratio between first and second quantity m : n = a : x, second and third quantity n : p = b : y, fourth and fifth quantity p : q = c : z, then m : n : p : q can be easily solved by using the trick shown below:


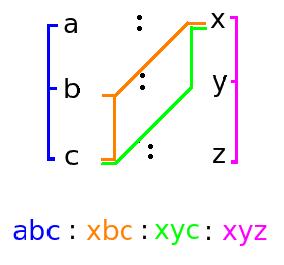m : n : p : q = abc : xbc: xyc : xyz

6) If a number a is divided in the ratio x : y,
1) First part: ax
(x + y)

2) Second part: ay
(x + y)


Question Variety

Type 1: Proportion


Examples:

Q 1. If a : b = 2 : 3 and b : c = 5 : 7, then find a : b : c.

a. 12 : 15 : 9
b. 10 : 15 : 21
c. 14 : 12 : 21
d. 2 : 15 : 7
View solution

Correct option : (b)

Here, to find a : b : c, use the trick discussed in quick tips and tricks.


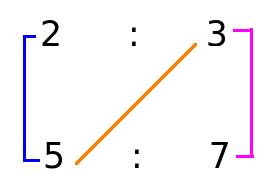
a : b : c = (2 x 5) : ( 3 x 5) : (3 x 7) = (10) : (15) : (21)


Q 2. If A : B : C = 3 : 4 : 7, then what is the ratio of (A / B) : (B / C) : (C / A)?

a. 63 : 48 : 196
b. 66 : 49 : 190
c. 56 : 40 : 186
d. 46 : 38 : 160
View solution

Correct option : (a)

Hint: If a = kb for some constant k, then we can say that a is directly proportional to b.
A : B : C = 3 : 4 : 7
Assume, A = 3 k, B = 4 k, C = 7 k

Therefore,

A = (3k), B = (4k), C = (7k)
B(4k)C(7k)A(3k)

A = (3), B = (4), C = (7)
B(4)C(7)A(3)

L.C.M of 3, 4, 7 is 84

(3 x 84) / 4 = 63
(4 x 84) / 7 = 48
(7 x 84) / 3 = 196

Ratio of (A/B) : (B/C) : (C/A) = 63:48:196

Type 2: Division and Distribution of objects into ratios


In this type of numericals, given amount or quantity is divided among two or more persons and amount or quantity retained by each person is calculated.

Examples:

Q 3. If Suresh distributes his pens in the ratio of 1/2 : 1/4 : 1/5 : 1/7 between his four friends A, B, C and D, then find the total number of pens Suresh should have?

a. 153
b. 150
c. 100
d. 125
View solution

Correct option : (a)

Here, A : B : C : D = 1 / 2 : 1 / 4 : 1 / 5 : 1 / 7

1) L.C.M of 2, 4, 5, 7 is 140
2) Find the number of pens each friend received --------- (To find no. of pens each friend has, multiply the ratio with the L.C.M. calculated)

A = (1/2) x 140 = 70
B = (1/4) x 140 = 35
C = (1/5) x 140 = 28
D = (1/7) x 140 = 20

3) Total number of pens = (70 x + 35 x + 28 x + 20 x) = 153 x
Minimum number of pens (x) = 1
Therefore, total number of pens = 153 pens.


Q 4. If Rs 1050 is divided into three parts, proportional to (1 / 3) : (3 / 4) : ( 4 / 6), then what is the first part?

a. 500
b. 300
c. 200
d. 100
View solution

Correct option : (c)

Given:

1050 = 1 : 3 : 4
346

1) L.C.M. of 3, 4 and 6 is 12

Therefore, multiply numerator and denominator of (1/3) with 4, to obtain denominator 12. Similarly multiply (3/4) with 3 and (4/6) with 2
4 : 9 : 8 = 4 : 9 : 8
121212

2) If a number a is divided in three ratios x : y : z,
First Part: ax ------- (a is the number divided)
(x + y + z)

Therefore,
First Part: (1050 x 4) = 200
(4 + 9 + 8)

Alternate method:
1050 = 1 : 3 : 4
346

L.C.M. = 12, therefore, multiply numerator and denominator of (1/3) with 4, to obtain denominator 12. Similary multiply (3/4) with 3 and (4/6) with 2
4 : 9 : 8 = 4 : 9 : 8
121212

Let m be one of the parts of 1050, therefore,
(4m + 9m + 8m) = 1050
12

Solving we get, m = 600
To calculate first part multiply m into first fraction (1/3) = 600 x1 = 200
3

Type 3: Mixture of different contents


Examples:

Q 5. In a mixture of 13 litres, the ratio of milk and water is 3 : 2. If 3 liters of this mixture is replaced by 3 liters of milk, then what will be the ratio of milk and water in the newly formed mixture?

a. 10 : 3
b. 8 : 5
c. 9 : 4
d. 1 : 1
View solution

Correct option: (c )

Given: Total quantity of mixture = 13 liters

3 litres of mixture is removed from the container – So, let's forget this altogether!
Now, you are left with only 10 litres of mixture in 3:2 ratio.

Milk in 10 litres mix = 10 x 3 = 6 litres
(2 + 3)

Water in 10 litres mix = 10 x 2 = 4 litres
(2 + 3)

We add 3 litres milk to this.

So, milk in new mix is = 6 liters + 3 litres = 9 litres
Water= 4 litres

Ratio of milk : water = 9 : 4


Q 6. A mixture contains alcohol and water in the ratio of 7 : 5. If 8 liters of water is added to the mixture, then the ratio becomes 7 : 9. Find the quantity of alcohol in the given mixture?

a. 15 liters
b. 14 liters
c. 19 liters
d. 21 liters
View solution

Correct option : (b)

1) Assume quantity of milk and water to be 7x and 5x.

2) Find the total quantity of mixture (x)

Therefore,

7x = 7
(5x + 8)9

Solving this we get the value of x = 2

3) Quantity of alcohol in the mixture = (7x) = (7 x 2) = 14 liters

Type 4: Income/ Expenditure and Salary


These questions are related to annual savings or expenditure. We are asked to find the salaries in ratio form or vice-versa.

Examples:

Q 7. The annual income of Puja, Hema and Jaya taken together is Rs. 46,000. Puja spends 70 % of income, Hema spends 80 % of her income and Jaya spends 92 % of her income. If their annual savings are 15 : 11 : 10, find the annual saving of Puja?

a. 10, 000 /-
b. 12, 000 /-
c. 17, 500 / -
d. 25, 000 /-
View solution

Correct option: (a)

Suppose income of Puja, Hema and Jaya are Rs A, Rs B and Rs C.
Annual income given is Rs 46, 000

If 70 % income is spent by Puja, then that means she saves 30 % (0.3). Similarly, Hema saves 20 % (0.2) and Jaya saves 8 % (0.08)

Given ratio of their annual savings are 15 : 11 : 10

(0.3A) = (0.2B) = (0.08C) = A = B = C
1511105055125
= A = B = C = (A + B + C) = 46000 ------ (Since, A + B + C = 46000)
101125(10 + 11 + 25)46

= 1000

From this equation, we can
A = 1000 x 10 = 10,000
B = 1000 x 11 = 11,000
C = 1000 x 25 = 25000


Q 8. A man, his wife and daughter worked in a graden. The man worked for 3 days, his wife for 2 days and daughter for 4 days. The ratio of daily wages for man to women is 5 : 4 and the ratio for man to daughter is 5 : 3. If their total earnings is mounted to Rs. 105, then find the daily wage of the daughter.

a. Rs. 15
b. Rs. 12
c. Rs. 10
d. Rs. 9
View solution

Correct option (d)

Assume that the daily wages of man, women and daughter are Rs 5x, Rs. 4x, Rs 3x respectively.
Multiply (no. of days) with (assumed daily wage) of each person to calculate the value of x.
[3 x (5x)] + [2 x (4x)] + [4 x (3x)] = 105
[15x + 8x + 12x] = 105
35x = 105
x = 3
Hence, man's daily wage = 5x = 5 x 3 = Rs. 15
Wife's daily wage = 4x = 4 x 3 = Rs. 12
Daughter's daily wage = 3x = 3 x 3 = Rs. 9


Q 9. Amit, Raju and Ram agree to pay their total electricity bill in the proportion 3 : 4 : 5. Amit pays first day's bill of Rs. 50, Raju pays second day's bill of Rs. 55 and Ram pays third day's bill of Rs. 75. How much amount should Amit pay to settle the accounts?

a. Rs. 15.25
b. Rs. 17
c. Rs. 12
d. Rs. 5
View solution

Correct option: (d)

Toatal bill paid by Amit, Raju and Ram = ( 50 + 55 +75 ) = Rs. 180
Let amount paid by Amit, Raju and Ram be Rs. 3x, 4x and 5x respectively.
Therefore, (3x + 4x + 5x ) = 180
12x = 180
x = 15
Therefore, amount paid by,
Amit = Rs. 45
Raju = Rs. 60
Ram = Rs. 75
But actually as given in the question, Amit pays Rs. 50, Raju pays Rs. 55 and Ram pays Rs. 80. Hence, Amit pays Rs. 5 less than the actual amount to be paid. Hence he needs to pay Rs. 5 to Raju settle the amount.


Q 10. Salaries of Ram and Sham are in the ratio of 4 : 5. If the salary of each is increased by Rs. 5000, then the new ratio becomes 50 : 60. What is Sham's present salary?

a. Rs. 20,000
b. Rs. 25,000
c. Rs. 30,000
d. Rs. 35,000
View solution

Correct option: (c)

Assume original salaries of Ram and Sham as 4x and 5x respectively.

Therefore,

(4x + 5000) = 50
(5x + 5000)60

60 (4x + 5000) = 50 (5x + 5000)
10 x = 50,000
5x = 25, 000
Sham's present salary = 5x + 5000 = 25,000 + 5000
Sham's present salary = Rs. 30,000

Type 5: Coins and Values


These are ratio based numericals, in which a bag containing different number of coins like 10 p, 50, 25 p are given along with the total amount and we are asked to find each type of coin in the bag or the value of coins.

Examples:

Q 11. A bag contains equal number of 25 paise, 50 paise and one rupee coins respectively. If the total value is Rs 105, how many types of each type are present?

a. 75 coins
b. 60 coins
c. 30 coins
d. 25 coins
View solution

Correct option: (b)

Bag consists of 25 paise, 50 paise and 1 rupee (100 paise) so the ratio becomes 25 : 50 : 100 or 1 : 2 : 4

Total value of 25 paise coins =(1 / 7 ) x 105 = 15
Total value of 50 paise coins = (2 / 7) x 105 = 30
Total value of 100 paise coins = (4 / 7) x 105 = 60

No. of 25 paise coins = 15 x 4 = 60 coins
No. of 50 paise coins = 30 x 2 = 60 coins
No. of 1 rupee coins = 60 x 1 = 60 coins

Therefore, there are 60 number of coins of each type.


Q 12. A purse contains 342 coins consisting of one rupees, 50 paise and 25 paise coins. If their values are in the ratio of 11 : 9 : 5 then find the number of 50 paise coins?

a. 180
b. 150
c. 162
d. 99
View solution

Correct option :(c)

Let the value of one rupee, 50 paise and 25 paise be 11x, 9x, 5x respectively.

No. of 1 rupee coins = (11x / 1) =11x
No. of 50 paise coins = (9x / 0.5) = 18x
No. of 25 paise coins = (5x / 0.25) = 20x

11x + 18x + 9x = 342
38x = 342
x = 9

Therefore, no. of 1 rupee coins = 11 x 9 = 99 coins
No. of 50 paise coins = 18 x 9 = 162 coins
No. of 25 paise coins = 20 x 9 = 180 coins



Practice questions on Ratio and Proportion
Problems on Chain Rule - Aptitude test, questions, shortcuts, solved example videos
Problems on Chain Rule - Quantitative aptitude tutorial with easy tricks, tips, short cuts explaining the concepts. Online aptitude preparation material with practice question bank, examples, solutions and explanations. Video lectures to prepare quantitative aptitude for placement tests, competitive exams like MBA, Bank exams, RBI, IBPS, SSC, SBI, RRB, Railway, LIC, MAT. Very useful for freshers, engineers, software developers taking entrance exams. Learn and take practice tests!
Pipes and Cisterns - Aptitude test, questions, shortcuts, solved example videos
Pipes & Cisterns - Quantitative aptitude tutorial with easy tricks, tips, short cuts explaining the concepts. Online aptitude preparation material with practice question bank, examples, solutions and explanations. Video lectures to prepare quantitative aptitude for placement tests and competitive exams like MBA, Bank exams, RBI, IBPS, SSC, SBI, RRB, Railway, LIC, MAT. Very useful for freshers, engineers, software developers taking entrance exams. Learn and take practice tests!
Boats and Streams - Aptitude test, questions, shortcuts, solved example videos
Boats and Streams - Quantitative aptitude tutorial with easy tricks, tips, short cuts explaining the concepts. Online aptitude preparation material with practice question bank, examples, solutions and explanations. Video lectures to prepare quantitative aptitude for placement tests and competitive exams like MBA, Bank exams, RBI, IBPS, SSC, SBI, RRB, Railway, LIC, MAT. Very useful for freshers, engineers, software developers taking entrance exams. Learn and take practice tests!
Post your comment
Discussion Board
Q7.
Q7. should be corrected to annual salary of Puja?
Aditi 06-29-2021
Easier and Similar solution for Q.7
Let us assume that their savings are 8k,9k and 20k respectively.
A spends 80% of his salary. Thus he saves (100-80=20%) of his salary.
So, 20%=8k
Therefore, A''s total salary i.e., 100%=40k
B spends 85% of his salary. Thus he saves (100-85=15%) of his salary. So, 15%=9k
Therefore, B''s total salary i.e., 100%=60k
C spends 75% of his salary. Thus he saves (100-75=25%) of his salary. So, 25%=20k
Therefore, C''s total salary i.e., 100%=80k
According to the question,
40k+60k+80k=1,44,000
k=800
Thus, C''s salary = 80k=80×800=64,000
Aditi 06-29-2021
Ratio and proportion
Find the third proportional of 2,8?

a. 64. b.32. C. 1/2. D.2
Princy 07-13-2020
Question no 12
"A purse contain 342 coins" instead of use "A purse contain 441 coins";then provided solution is correct.
shrikant koli 06-11-2020
Ratio and proportion
Amit, Raju and Ram agree to pay their total electricity bill in the proportion 3 : 4 : 5. Amit pays first day''s bill of Rs. 50, Raju pays second day''s bill of Rs. 55 and Ram pays third day''s bill of Rs. 75. How much amount should Amit pay to settle the accounts?

a. Rs. 15.25
b. Rs. 17
c. Rs. 12
d. Rs. 5
View solution
Correct option: (d)

Toatal bill paid by Amit, Raju and Ram = ( 50 + 55 +75 ) = Rs. 180
Let amount paid by Amit, Raju and Ram be Rs. 3x, 4x and 5x respectively.
Therefore, (3x + 4x + 5x ) = 180
12x = 180
x = 15
Therefore, amount paid by,
Amit = Rs. 45
Raju = Rs. 60
Ram = Rs. 75
But actually as given in the question, Amit pays Rs. 50, Raju pays Rs. 55 and Ram pays Rs. 80. Hence, Amit pays Rs. 5 less than the actual amount to be paid. Hence he needs to pay Rs. 5 to Raju settle the amount.
Correction Amit has paid 50 i.e., 5 more than what he actually has to pay. So Raju has to pay Amit 5
Darshitha 07-29-2019
Query on Q12
Hello,
I was solving the question number 12 when I came with an error and checked for the solution. The sum of the number of coins is 342. So that accounts for 11x+18x + 20 x = 49x, where x is constant. However, in solution, the number of 25p coins is summed up as 9x. Am I missing something here? Any help will be appreciated.
susmitha shankar 07-10-2019
Thank You
Thanks a lot for making these videos.
Souvik Ganguly 09-16-2018
Hi....
if x=(1\4)y and y=(1/5)z then x:y:z is equal to
Santha 10-6-2017

Related Content

Follow us

▲