Video on Surds and Indices - shortcuts, tips and tricksSurds and Indices
Before solving the numerical on this chapter make sure that you are perfect with the chapter of square and square roots, simplification, linear and quadratic equations and decimal fractions.
Important TermsSurd: Number which cannot be expressed in the fraction form of two integers is called as surd. Hence, the numbers in the form of
3,
32, …….
nx| For example: | 1 | can be written as | 1 | but 3 cannot be written in the form of fraction |
| 9 | 3 |
Irrational numbers which contain the radical sign (
) are called as surds.
Indices: Indices refers to the power to which a number is raised. Index is used to show that a number is repeatedly multiplied by itself.
For example: a
3 is a number with an index of 3 and base ‘a’. It is called as
“a to the power of 3” Quick Tips and Tricks1) The laws of indices and surds are to be remembered to solve problems on surds and indices. Laws of Indices1) x
m × x
n = a
m+n2) (x
m)
n = x
mn3) (xy)
n = x
ny
n| 5) | 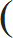 | x |  | n | = | xn |
| y | | yn |
Laws of Surds1)
nx = x
(1/n)2)
nxy =
nx ×
ny4) (
nx)
n = X
5)
mnx =
mnx6) (
nx)
m = (
nxm)
2) Expressing a number in radical formExample: l x
(m/n) l =
nxmThe exponential form l x
(m/n) l is expressed in radical form as
nxmImportant points to Remember 1) Any number raised to the power zero is always equals to one. (Eg: x
0 = 1)
2) Surd
nx can be simplified if factor of x is a perfect square
3) If denominator in a fraction has any surds, then rationalize the denominator by multiplying both numerator and denominator by a conjugate surd.
4) Every surd is an irrational number, but every irrational number is not a surd.
5) The conjugate of (2 + 7i) is (2 – 7i)
6) Different expressions can be simplified by rationalizing the denominator and eliminating the surd.
Rationalizing the denominator: To rationalize the denominator
7 multiply with its conjugate to both numerator and denominator
| Example 1: | 1 | = | 1 | × | 7 | = | 7 |
| 7 | 7 | 7 | 7 |
| Example 2: | 1 | = | 1 | × | 7 – 3 | = | 7 – 3 |
| 7 + 3 | 7 + 3 | 7 – 3 | 4 |
Types of Questions: Type 1: Simplify the given expressions using laws of indices and surds.
(1331)
– (2/3) View solution Correct Option: (c)
Cube root of 1331 is 11. Therefore,
(113)– (2/3)
Hint:
Remember the law of indices (xm)n = xmn
(11) – 3 × (2/3) = 11–2
Hint:
| Hence, 11–2 = | 1 | = | 1 |
| 112 | 121 |
| Q 2. | (32)(n/5) × 22n + 1 |
| 4n × 2n – 1 |
a. 4
b. 8
c. 2
nd. 2
n + 1View solution Correct Option: (a)
32 = 25 and 4 = 22
Substituting these values, we get
| (32)(n/5) × 22n + 1 | = | (25)(n/5) × 22n + 1 |
| 4n × 2n – 1 | (22)n × 2n – 1 |
Hint: Laws of indices (x
m)
n = x
mn and x
m × x
n = a
m + n| (25)(n/5) × 22n + 1 | = | (2) 5 × (n/5) × 22n + 1 | = | 2n × 22n + 1 |
| (22)n × 2n – 1 | 22n × 2n – 1 | 22n × 2a – 1 |
In the expression, bases are same, hence add the indices.| 2n × 22n + 1 | = | 2n + 2n + 1 | = | 23n + 1 |
| 22n × 2n – 1 | 22n + n – 1 | 23n – 1 |
| 23n + 1 | = 23n + 1 – (3n – 1) = 22 = 4 |
| 23n – 1 |
| Q 3. Find the value of | 1 | + | 1 | + | 1 |
| 125–(2/3) | 625–(3/4) | 729–(3/6) |
a. 132
b. 177
c. 185
d. 225
View solution Correct Option: (b)
53 = 125, 54 = 625, 36 = 729
| 1 | + | 1 | + | 1 |
| (53)–(2/3) | (54)–(3/4) | (36)–(3/6) |
Hint: Law of indices (x
m)
n = x
mnTherefore,
| 1 | + | 1 | + | 1 | = 52 + 53 + 33 = 177 |
| (5)–2 | (5)–3 | (3)–3 |