Video on Decimal - shortcuts, tips and tricksDecimal Fractions
Points to Remember1) Fraction: It represents a part of a whole or more generally, any number of equal parts. If a unit is divided into any number of equal parts, then one or more of these parts is termed as a fraction of the unit.
The numerator in a fraction represents a number of equal parts and denominator (≠0) represents how many of those parts make up a unit or a whole.
2) The value of fraction (x/y) = 1, if numerator = denominator
3) The value of fraction is zero,if numerator=0 and denominator ≠0
4) The value of fraction is infinity,if the denominator=0
5)The value of fraction remains unchanged,even if the
numerator and denominator are multiplied or divided by same number6) Pure recurring decimal: In a decimal fraction, if all the numbers after decimal point repeat, then it is called as pure recurring decimal.
7) Mixed recurring decimal: In a decimal fraction, if some numbers are repetitive and some are not, then it is called as mixed recurring decimal.
Basic Formulae: (Must Remember)
1) (a - b)
2 = (a
2 + b
2 - 2ab)
2) (a + b)
2 = (a
2 + b
2 + 2ab)
3) (a + b) (a – b) = (a
2 – b
2 )
4) (a
3 + b
3) = (a + b) (a
2 – ab + b
2)
5) (a
3 - b
3) = (a - b) (a
2 – ab + b
2)
6) (a + b + c)
2 = a
2 + b
2 + c
2 + 2 (ab + bc + ca)
7) (a
3 + b
3 + c
3 – 3abc) = (a + b + c) (a
2 + b
2 + c
2 – ab – bc – ac)
Operations on decimal fractions:
Here different operations performed on decimal fractions along with certain examples are given. Clear the concepts point by point and then move further to quick tips and tricks. Points covered: 1) Addition and subtraction of decimal fractions
2) Multiplication of decimal fractions by power of 10.
3) Multiplication of decimal fractions.
4) Decimal fraction ÷ Counting number
5) Decimal fraction ÷ Decimal fraction
1) Addition and subtraction of decimal fractionsTo add or subtract the decimal fractions, numbers are placed under each other in such a way, that the decimal points lie in one column.
Eg: 12.361 + 0.236 + 1236.1
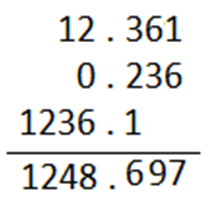2) Multiplication of decimal fractions by power of 10. The decimal point in the given number is shifted as many places as is the power of 10.
Eg: 4.236 × 100 = 423.6 or 0.563 × 1000 = 563
3) Multiplication of decimal fractions. Multiply the given numbers without considering the decimal points. Now mark the decimal point in the product by calculating the sum of number of decimal places in the given numbers.
Eg: 0.5 × 0.03 × 0.83
5 × 3 × 83 = 1245
No. of decimal places = 1 + 2 + 2 = 5
Now mark the decimal point after 5 places starting from left.
Answer = 0.012454) Division of a decimal fraction Divide the given numbers without considering the decimal points. Now mark the decimal point in the quotient obtained, by calculating the number of decimal places in the dividend.
Eg: (0.0133 ÷ 19)
(133 ÷ 19)=7
Dividend contains 4 places of decimal. Hence, the answer is 0.00075) Decimal fraction ÷ Decimal fractionEg: Divide 0.00025 by 0.5
Convert 0.5 without decimal place i.e. 5. Multiply numerator and denominator by 10.
Therefore, we get
=0.0025 ÷ 5
=0.0005
Comparison of fractions| If fraction in the form | 4 | , | 7 |
| 5 | 8 |
are to be compared or are to be arranged in ascending of descending order,Then simply convert these fractions into decimal form and then compare.
| Eg: Arrange | 4 | , | 3 | , | 6 | in descending order |
| 5 | 5 | 8 |
4/5 = 0.8, 3/5 = 0.6, 6/8 = 0.75
0.8 > 0.75 > 0.6, hence (4/5) > (6/8) > (3/5)
Concept of Pure Recurring Decimal If in a decimal fraction all the numbers after decimal point repeat, then it is called as pure recurring decimal.
In decimal fraction 23.6666, 6666 are repeating and hence the fraction is called as recurring decimal.
How to convert a
Pure Recurring Decimal into Vulgar Fractions? In a decimal fraction, if there are n numbers of repeated numbers after a decimal point, then just write one repeated number in the numerator and in denominator take n number of nines equal to repeated numbers you observe after the decimal point. Let’s see an example, to easily understand the conversion
0.
8 =0.8888…,this means only
one number repeats.As discussed, numerator is taken as 8 which is the single repeated number after the decimal point and denominator is taken as 9, because there is only one number which repeats after decimal point.
0.
57 =0.575757…..,this means 57 is a
set of number which repeats
Numerator is taken as 57 (one repeated set) and denominator is taken as 99, (because two numbers 5 and 7 repeat after the decimal point)
How to convert Mixed Recurring Decimal into Vulgar Fraction? REMEMBER: Numerator = (All digits after decimal point) Repeated digits only once –
(Non-repetitive digit after decimal point)Denominator = Take 9 as many times the
repetitive digit, followed by
zeros equal to number of non-repetitive digits. Check whether you have got the correct answer, by dividing the numerator by denominator of the obtained vulgar fraction. Example: 0.23434
This is an example of mixed recurring decimal, because after the decimal point number 2 does not repeat and numbers 3 and 4 repeat. This type of number can be converted into fraction as follows:
0.23434… =0.2
34| 0.234 = conversion of mixed recurring decimal into vulgar fraction = | 232 |
| 990 |
Question Variety Type1: Find the fractions in ascending or descending order
Which of the following has fractions in ascending order?
View solution Correct Option: (d)
Convert fractions into decimal form. These calculations are to be solved quickly in mind otherwise will require a lot time.
Option 1: 0.4, 0.6, 0.33, 0.5, 0.8 --- (wrong)
Option 2: 0.3, 0.4, 0.6, 0.8, 0.5 --- (wrong)
Option 3: 0.3, 0.4, 0.8 , 0.5, 0.6 --- (wrong)
Option 4: 0.33, 0.4, 0.5, 0.6, 0.8 --- (correct)
0.33 < 0.4 < 0.5 < 0.6 < 0.8 ---- (Ascending order)
Which of the following has fractions in descending order?
View solution Correct Option: (b)
Convert fractions into decimal form. These calculations are to be solved quickly in mind otherwise will require a lot time.
Option 1: 0.8, 0.5, 0.4, 0.6, 0.33--- (wrong)
Option 2: 0.8, 0.6, 0.5, 0.4, 0.3 --- (correct)
Option 3: 0.5, 0.3, 0.4 , 0.8, 0.6 --- (wrong)
Option 4: 0.33, 0.4, 0.5, 0.6, 0.8 --- (wrong)
0.8 > 0.6 > 0.5 > 0.4 > 0.3 ---- (Descending order)
