Home >
Aptitude test > Height and Distance
Height
and Distance - Number of questions : 30 - April 22, 2013 at 08:50 AM by
Prateek Bajpai
Height
and Distance - Number of questions : 20 - April 23, 2013 at 12:16
PM by Shashank Chaturvedi
Height and Distance - Posted on August 02, 2013 at 01:10 PM by
Rahul Choudhary
1) The angle of elevation of the sun is 60°. Find the length of the shadow
of a man who is 180 cm tall.
a) 127.27 cm
b) 103.92 cm
c) 311.77 cm
d) None of these
View Answer / Hide Answer
ANSWER : 103.92 cm
SOLUTION :
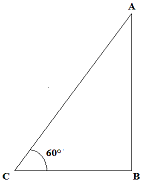
Let AB be the man and BC be his shadow
AB = 180
tan60° = AB/BC
v3 = 180/BC
BC = 103.92 cm
2) What is the distance between a tower and an observer if the angle of
elevation from the observer’s eye to the top of the tower (height = 50 m) is
30°? The observer is 1.5 m tall.
a)84
b)28
c)30
d)90
View Answer / Hide Answer
ANSWER : 84
SOLUTION :
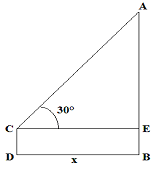
Let AB be the tower and CD be the observer
tan30° = AE/CE
1/v3 = (AB – CD) / x = (50 – 1.5)/ x = 48.5/x
x = 84 m
3) Two boats are spotted on the two sides of a light house. If the angle of
depression made by both the boats from top of the lighthouse is 30° and 45° and
the height of the light house is 125 m then find the distance between the two
boats.
a)1
b)188.56 m
c)250 m
d)197.17 m
View Answer / Hide Answer
ANSWER : 197.17 m
SOLUTION :
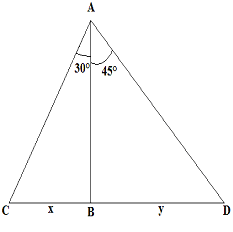
Let AB be the light house and the two boats be at C and D
AB = 125 m
tan30° = BC/AB = x/125 = 1/v3
x = 72.17 m
tan45° = BD/AB = y/125 = 1
y = 125 m
Therefore, the distance between the two boats is = x + y
= 72.17 + 125
= 197.17 m
4) A man standing on the terrace of a building watches a car speeding
towards him. If at that particular instant the car is 200 m away from the
building makes an angle of depression of 60° with the man’s eye and after 8
seconds the angle of depression is 30°, what is the speed of the car?
a)15 m/s
b)16.67 m/s
c)25 m/s
d)Cannot be determined
View Answer / Hide Answer
ANSWER : 16.67 m/s
SOLUTION :
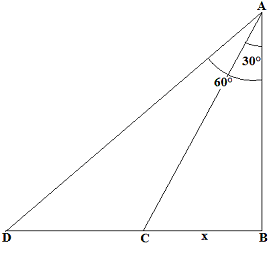
Let AB be the building and the man is standing at A.
When the car is 200m away from the building, the angle of depression is 60°
tan60 = BD/AB = v3
200/AB = v3
AB = 115.47 m
tan30° =BC/AB = x/115.47 = 1/v3
x = 66.67
Now, the car travels distance CD in 8 seconds
CD = BD – BC = 200 – 66.67 = 133.33 m
Speed = 133.33/8 = 16.67 m/s
5) A ship is approaching an observation tower. If the time taken by the ship
to change the angle of elevation from 30° to 45° is 10 minutes, then find the
time the ship will take to cover the remaining distance and reach the
observation tower assuming the ship to be travelling at a uniform speed.
a) 15 minutes 20 seconds
b) 13 minutes 40 seconds
c) 16 minutes 40 seconds
d) Cannot be determined
View Answer / Hide Answer
ANSWER : 13 minutes 40 seconds
SOLUTION :
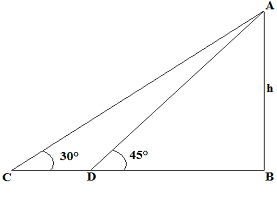
Let AB be the observation tower and h be its height.
Also, let the ship be at C when the angle of elevation is 30° and at D when the
angle of elevation is 45°.
The time taken by the ship to travel from C to D is 10 minutes and we need to
find out the time the ship will take to reach B from D.
tan30 = AB/CB = h/CB = 1/v3
CB = v3*h
tan45 = AB/DB = h/DB = 1
DB = h
CD = CB – DB = (v3h – h) = h(v3 – 1)
Now, as h(v3 – 1) distance is covered in 10 minutes, a distance
of h is covered in = 13.66 minutes = 13 minutes 40 seconds
6) On the two sides of a road are two tall buildings exactly opposite to
each other. The height of the taller building is 60 m. If the angle of
elevation from the top of the smaller building to the top of the taller one is
30° and the angle of depression from top of the taller building to the foot of
the smaller one is 30°, then find the height of the smaller building.
a) 45
b) 30
c) 40
d) 20
View Answer / Hide Answer
ANSWER : 40
SOLUTION :
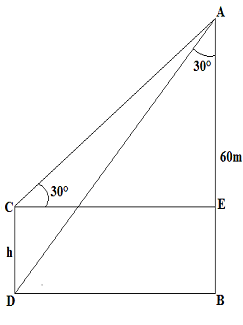
Let AB be the taller building of height 60m and CD be the smaller one of height
h m.
tan30= DB/AB = DB/60 = 1/v3
DB = 34.64 m
tan30= AE/CE = AE/DB = 1/v3 = AE/34.64
AE = 60 – h = 20
h = 40 m
Sample questions on Height and Distance
The angle of elevation of the sun, when the length of the shadow of a tree is 1
times the height of the tree, is:
30
45
60
90
The angle of elevation of the sun, when the length of the shadow of a tree is 1
times the height of the tree, is:
30
45
60
90
A train can travel 50% faster than a car. Both start from point A at the same
time and reach point B 75 kms away from A at the same time. On the way,
however, the train lost about 12.5 minutes while stopping at the stations. The
speed of the car is:
100 km/hr
110 km/hr
120 km/hr
130 km/hr
A little boy is flying a kite. The string of the kite makes an angle of 30°
with the ground. If the height of the kite is h = 24 m, find the length (in
meters) of the string that the boy has used.
48
50
52
54
A pole of height h = 50 ft has a shadow of length l = 28.87 ft at a particular
instant of time. Find the angle of elevation (in degrees) of the sun at this
point of time.
30
45
60
90
The height of the tree is 5 meters and the length of the shadow is 2 meters,
find the angle of elevation of the sun
30 degree
45 degree
60 degree
90 degree
A tree of height 100m has a shadow of length 100 m at a particular instant of
the day. Find the angle of elevation of the sun at this point of time.
45 degree
30 degree
60 degree
90 degree
|