Logarithm - Aptitude test, questions, shortcuts, solved example videos

Logarithms - Aptitude test, questions, shortcuts, solved example videos

Logarithm - tips, tricks and questions

Logarithms make math easy. Studying this chapter will help you in solving and simplifying complicated numerical expressions. Rules of logarithm can also be used to find the square and square root of numbers.

Important terms:

Logarithm: It is the power to which a number must be raised in order to get some other number.

Common logarithm:Logarithms with base 10 are common logarithms.
Common logarithms are written as log10 x and if any expression is not indicated with a base, then base 10 is considered.

Natural logarithm: Logarithms with base e are natural logarithms.
Natural logarithms are written as logex and denoted as ln (x).

Logarithm of a number contains 2 parts: Characteristic and Mantissa

Characteristic is an integral part of logarithm.

Case 1: If number is greater than 1.
In this condition, characteristic is considered as one less than the number of digits in the left of decimal point in the given number.

Example: 256.23
Number of digits to the left of decimal point are 3. Hence, the characteristic is one less than number of digits before decimal points i.e 2.

Case 2: If number is less than 1.
In this condition, characteristic is considered as one more than the number of zeros between decimal point and first digit of the number. It is negative and is denoted as
(One bar) 1 or (Tow bar) 2

Example: 0.00735
Number of zeros between decimal point and first significant digit 7 are 2. Hence the characteristic is one more than number of zeros i.e 3

Mantissa: It is the decimal part of logarithm. Log table is used to find the mantissa.

Quick Tips and Tricks

Very Important: If base is not mentioned, then always remember to take it as 10.

Properties of logarithm

1) logxx = 1

2) loga1 = 0

3) alogax = x
4) logax1
logxa

5) loga(xP) = p (logax)
6) logax = logbx = log x - - - (Change of base formula)
logba log a
7) loga x = logax – logby - - - - (Division Rule)
y

8) loga (xy) = loga x + logb y

Important points to remember

1) Logarithms are opposite to exponentials which means logs are inverses of exponentials.

2) Given logarithmic form can be converted into exponential form as shown below:

b = base y = exponent x = answer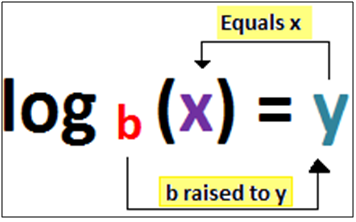



Exponential form: by = x

Logarithm form: logb (x) = y

Log of numbers (2 – 10) (Must Remember)

Log 2 = 0.301
Log 3 = 0.477= 0.48
Log 4 = 0.60
Log 5 = 0.698 = 0.7
Log 6 = 0.778 = 0.78
Log 7 = 0.845 = 0.85
Log 8 = 0.90
Log 9 = 0.954= 0.96
Log 10 = 1

Finding log without using calculator

These are very easy methods to find the log of numbers without calculator.

Step 1: You should know all the prime factors of given numbers.
Step 2: Method 2: Log of 4 to 9 can be easily determined if only the value of log 2 and log 3 is remembered.

Method 1Method 2
Log of composite number (x) = Sum of logarithms of its prime factors.

Example: Log of 9 =?
If you know the value of log 3, the value of log 9 can be easily determined.
Log 3 = 0.477
Log of 9 = Sum of logarithms of its prime factors.
Log of 9 = log 3 + log 3
= 0.477 + 0.477
= 0.954
Log of 9 = 0.954		 Log 2 = 0.301
Log 3 = 0.477
Log 4 = 2 x log 2 = 0.60206
Log 5 = 1 – log 2 = 0.6989
Log 6 = log 2 + log 3 = 0.778
Log 7 = 0.84510 --- (Remember)
Log 8 = 3 x log 2 = 0.9030
Log 9 = 2 x log 3 = 0.9542

Types of Questions

Type 1: Find the value of given expression.


Q 1. log2 64

a. 6
b. 8
c. 16
d. 32
View solution

Correct Option: (a)

We have to simplify the given expression, which means in exponential form. Remember the tricks discussed above.
Hint:
Logarithm form: logb (x) = y
Exponential form: by = x

Given: log2 64
Let the solution of log2 64 be y.
Log2 64 = y
2y = 64
26 = 64
Therefore, y = 6

Q 2. log71
2401

a. 7
b. -3
c. - 4
d. 9
View solution

Correct Option: (c)

We have to simplify the given expression, which means in exponential form. Remember the tricks discussed above.
Hint:
Logarithm form: logb (x) = y
Exponential form: by = x

Let the solution of log71 be y
2401
log71 = y
2401
7 y = 1 = 1 = 7–4
240174

Therefore,
y=-4


Q 3. 49log74

a. 7
b. 14
c. 16
d. 18
View solution

Correct Option: (c)

Hint:
alogax = x, here the base of logax and number which is based to logax are same. i.e. a

Therefore, in the given expression
49log74 = (72)log74

loga(xp) = p(logax)

Carefully understand the simplification done using the properties of logarithm.
(7 2) log74 = (7) (log74)2 = (7) log7(4 2)

We know that, alogax = x

Hence, (7) log7(42) = 42 = 16

Type 2: Simpify

Q 4. Simplify:1 + 1 + 1
logab (abc)logbc(abc)logac(abc)

a. 0
b. 1
c. 2
d. abc
View solution

Correct Option: (c)

Hint:

logax = 1
logxa
1 + 1 + 1
logab (abc)logbc(abc)logac(abc)

logabc(ab) + logabc(bc) + logabc(ac)

Now use the product rule:
logaxy = logax + logay

logabc(ab × bc × ac) = logabc(abc) 2
= 2 logabc(abc)

We know that, logxx = 1

Therefore,
2 logabc(abc) = 2 × 1 = 2


Q 5. Simplify: log43 × log24364

a. 3/5
b. 2/5
c. 3/4
d. 1/3
View solution

Correct Option: (a)

Hint:

Change of base formula: logax = logbx = log x
logbalog a

log43 × log24364
= log 3 × log 64
log 4 log 243
= log 3 × log (43)
log 4 log (35)

loga(xp) = p(logax)
= log 3 × 3(log 4)
log 4 5(log 3)
= 3
5


Q 6. If xa = yb, then
a. log x = a
log yy
b. log x = b
log ya
c. log x = ab
log y
d. None of these
View solution

Correct Option: (b)

Given:
xa = yb
Take log on both the sides, we get
log xa = log yb
a(log x) = b(log y)

log x = b
log ya

Type 3: Find the value of x

Q 7. If log8x = 24, then find the value of x
3

a. 16
b. 32
c. 56
d. 66
View solution

Correct Option: (b)

The given expression is given in logarithmic form. To find the value of x, convert this expression in exponential form.

Hint:
If Logarithm form is logb (x) = y, then Exponential form is by = x

Logarithmic form = log8x = 24 = 10
33
Therefore,
Exponential form = (8)(10/3) = x
= (2(3/2))(10/3) = 2((3/2) × (10/3)) = 25 = 32


Q 8. Find the value of x which satisfies the given expression [log10 2 + log (4x + 1) = log (x + 2) + 1]

a. 6
b. 7
c. - 6
d. - 9
View solution

Correct Option: (d)

Hint:
If base is not mentioned, then always remember to take it as 10.
Hence, in the given expression, assume base as 10
We are given, [log10 2 + log10 (4x + 1) = log10 (x + 2) + 1]
[log10 2 + log10 (4x + 1) = log10 (x + 2) + 1]
[log10 2 + log10 (4x + 1) = log10 (x + 2) + log1010]
Now, Use the product rule: loga(xy) = logax + logay
[log10 2 (4x + 1)] = [log10 10(x + 2)]
(4x + 1) = (5x + 10)
4x + 1 = 5x + 10
x = - 9


Q 9. Find the value of log (8. 363), if log 2 = x, log 3 = y and log 7 = z
a. 4x + 1z + 2y
33
b. 2x + 1z + 1y
33
c. 3x + 1z + 2y
33
d. x + 1z + 2y
33
View solution

Correct Option: (c)

Hint:
Use the product rule: loga(xy) = logax + logay
log (8. 363)
= log 8 + log363
= log 8 + log63(1/3)
= log 23 + log(7 × 32)(1/3)
= 3 log 2 + (1/3) log 7 + (2/3) log 3

We are given that, log 2 = x, log 3 = y and log 7 =z

= 3x + 1z + 2y
33
Post your comment
Discussion Board
Permutations and Combinations
I refer to the following question in Permutation and combinations. Q 7. A bag contains 2 white marbles, 3 black marbles and 4 red marbles. Find in how many ways, 3 marbles can be drawn, so that at least one black marble is included in each draw?


I am struggling to understand how there could be 64 ways as per solutions. The colours of the marbles are repeated. So even though there may be 64 ways, the repeats have to be discounted.

If we did it manually, the only combinations you could have are:

1) black x 1 red x 1, white x 1
2) black x 1 red x 2
3) black x 1 white x 2

4) black x 2 red x 1
5) black x 2 white x 1

6) black x 3

Assuming I am right about discounting repeats, then I run into trouble trying to incorporate it. For Scenario 1: ie 1 black and 2 other colours. I would get a formula that looks like this:

3!/(2!x3!) X 6!/[(4! x 2!) x (2! x 4!)] = 5/32

ie black repeat 3!, white repeat 2! red repeat 4!

Please help! :)

kath gumtree 07-30-2019

Related Content

Follow us

▲