|
Video on Problems on Percentage - shortcuts, tips and tricksPercentagePoints to Remember| 1) Y % is expressed as | Y | | 100 |
| 2) To find percent of | x | = | 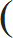 | x | × 100 | 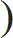 | % | | y | y |
Quick Tips and Tricks 1. Prices of Goods (1) If the price of goods increases by R %, then the reduction in consumption so as not to increase the expenditure can be calculated using the formula:  | R | × 100 |  | % | | (100 + R) |
(2) If the price of goods decreases by R %, then the increase in consumption so as not to decrease the expenditure can be calculated using the formula:  | R | × 100 |  | % | | (100 – R) |
2. Numerical on Population: Population of a city at present is P and it increases at the rate of R% per annum. | (1) To find population after n years = P |  | 1 + | R |  | n | | 100 |
| -------- (After n years population increases, thus |  | 1 + | R |  | is used) | | 100 |
| (2) To find population n years ago = | | | P |  | 1 + | R |  | n | | 100 |
|
3. Numerical on Depreciation: Present value of machine is M, If it depreciates at the rate of R% per annum. | (1) To find value of machine after n years = P |  | 1 – | R |  | n | | 100 |
| -------- (After n years the value of machine decreases, thus |  | 1 – | R |  | is used) | | 100 |
| (2) To find the value of machine n years ago = | | | P |  | 1 – | R |  | n | | 100 |
|
Question VarietyGenerally 5 types of questions are asked from this chapter. Understanding these concepts will help in solving the problems related to this chapter. Type 1: Numerical on numbers The difference between two numbers is 1550. If 8 % of one number is 10 % of the other number, then find the two numbers a. 4973, 6523 b. 5450, 7000 c. 6200, 7750 d. 6500, 4950 View solution Correct Option: (c)
Let two numbers be x and y.
It is given that, 8 % of x = 10 % of y
Therefore, Difference between two numbers (x – y)= 1550 Substituting the value of x, we get y=1550×4=6200 The two numbers whose difference is 1550 are 6200 and 7750. Two numbers P and Q are such that, the sum of 2 % of P and Sum of 2 % of Q is two-third of the sum of 2 % of P and 6 % of Q. Find the ratio of P and Q. a. 2 : 5 b. 3 : 1 c. 1 : 4 d. 5 : 1 View solution Correct Option: (b)
The sum of 2 % of P and Sum of 2% of Q is two-third of the sum of 2 % of P and 6 % of Q.
This sentence means that, | 2% of P + 2% of Q = | 2 | (2% of P + 6% of Q) | | 3 |
| 2 | P + | 2 | Q = | 2 | 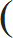 | 2 | P + | 6 | Q | 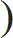 | | 100 | 100 | 3 | 100 | 100 |
| 1 | P + | 1 | Q = | 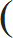 | 1 | P + | 1 | Q | 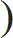 | | 50 | 50 | 75 | 25 |
Alternate method| 2 | P + | 2 | Q = | 2 | 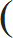 | 2 | P + | 6 | Q | 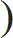 | | 100 | 100 | 3 | 100 | 100 |
Simply eliminate 100 from both the sides, we get 3(2P + 2Q) = 2(2P + 6Q) 6P + 6Q = 4P + 12Q 6P – 4P =12Q – 6Q 2P = 6Q 50 % of a number is 18 less than two-third of that number. Find the number. a. 123 b. 119 c. 115 d. 108 View solution Correct Option: (d)
Let the number be x.
It is given that, 50 % of a number is 18, less than two-third of that number. This means that, 50x=5400 x=108 The number is 108When 35 is subtracted from a number; it reduces to its 80 %. Find the four-fifth of that number. a. 140 b. 125 c. 137 d. 129 View solution Correct Option: (a)
We are given, 35 when subtracted from a number, reduces to its 80 %.
Therefore,
Let the number be x. Solving, we get the value of x Now, we are asked to find the four-fifth of that number i.e x Hence, the number is 140.
|
|
Type 2: Numerical on Depreciation The value of lathe machine depreciates at the rate of 10 % per annum. If the cost of machine at present is Rs. 160,000, then what will be its worth after 2 years? a. Rs. 122,365 b. Rs. 153,680 c. Rs. 129,600 d. Rs. 119,900 View solution Correct Option: (c)
Hint: Present value of machine is M. If the cost depreciates at the rate of R% per annum, then | The value of machine after n years = P |  | 1 – | R |  | n | | 100 |
In this numerical, we are given the present cost of the machine i.e 160,000 and the cost decreases by 10 % per annum. We have to find the cost of this machine after 2 years. We can solve this numerical in a minute, if we know the trick used to solve such numerical related to depreciation of cost. Given: Present amount = Rs. 1,60,000 Rate of depreciation = 10 % Substituting the given values, we get | The value of machine after n years = P |  | 1 – | R |  | n | | 100 |
| = 1,60,000 × |  | 1 – | 10 |  | 2 | | 100 |
= Rs. 129,600 After 2 years, the cost of machine = Rs. 129,600The value of Xerox machine depreciates at the rate of 10 % per annum. If the cost of machine at present is Rs. 75,000 then what was the value of machine before 2 years? a. Rs. 90,000 b. Rs. 92,600 c. Rs. 93,800 d. Rs. 95,000 View solution Correct Option: (b)
Hint: Present value of machine is M. If the cost depreciates at the rate of R% per annum, then | The value of machine n years ago = | | | P |  | 1 – | R |  | n | | 100 |
|
Given: Cost of Xerox machine at present = Rs. 75,000 Rate of depreciation = 10 % Substituting the given values, we get | The value of machine n years ago = | | | P |  | 1 – | R |  | n | | 100 |
|
| = | | | 75000 |  | 1 – | 10 |  | 2 | | 100 |
|
=Rs.92592.60 Therefore, the value of machine before 2 years = Rs. 92592.60 But this value is not available in the given options. Hence, select the nearby value to the amount of Rs. 92592.60. Among the listed options option (b) is the correct answer.
|
|
Type 3: Numerical on Population The current birth rate per thousand is 30, whereas corresponding death rate is 10 per thousand. Find the net growth rate in terms of population increase in percent. a. 1.5 % b. 2 % c. 2.5 % d. 3 % View solution Correct Option: (b)
We are given that,
1) Current birth rate per thousand is 30
2) Corresponding death rate is 10 per thousand
Hence, net growth on 1000 = Current birth rate - death rate
= 30 – 10 =20
We are asked to find, net growth rate in terms of population increase in percent (which means net growth on 100) | Net worth on 100 = | Net worth on 1000 | × 100 | | 1000 |
| Net worth on 100 = | 20 | × 100 = 2% | | 1000 |
The total population of a city is 6500.The number of males and females increases by 5 % and 10 % respectively and consequently the population becomes 7000. Find the number of males in the village. a. 4000 b. 3000 c. 3500 d. 2950 View solution Correct Option: (b)
We are given that,
1) Total population of city = 6500
2) Increase in male and female population = 5 % & 10% respectively.
3) Final population of city = 7000
Hence,
Let’s assume that number of males = x
Number of female = 6500 – x
Therefore, after increase in 5 % male and 10 % female, the population becomes 7000
5 % male +10 % female = Difference between new and original population | 5 | x + | 10 | (6500 – x) = 7000 – 6500 | | 100 | 100 |
5x+65000-10x=50000 5x= 15000 x=3000 Number of males = 3000
Number of females = 3500 The present population of a country is 10 crores. If it rises to 17.28 crores during next 3 years, then find uniform rate of growth in population. a. 20 % b. 30 % c. 40 % d. 60 % View solutionQ 10. The population of different trees in a field increased by 10 % in first year, increased by 8 % in second year and decreased by 10 % in third year. If at present the number of trees is 26730, then find the number of tress in the beginning. a. 30000 b. 25000 c. 27000 d. 27865 View solution Correct Option: (b)
Hint: | To find population n years ago = | | | P |  | 1 + | R |  | n | | 100 |
|
We are given, number of trees increased in 1) First year = increased by 10 % 2) Second year = increased by 8 % 3) Third year = decreased by 10 % Therefore, to find number of trees in the beginning use the trick. | Population n years ago = | | 26730 | |
 | 1 + | 10 |  |  | 1 + | 8 |  |  | 1 + | 10 |  | | 100 | 100 | 100 |
| |
| = 26730 × | 10 | × | 25 | × | 10 | | 11 | 27 | 9 |
= 25000
|
|
Type 4: Numerical on Prices of Goods The price of diesel increases by 50 %. Find by how much percent a truck owner must reduce his consumption in order to maintain the same budget? a. 11.11 % b. 22.22 % c. 33.33 % d. 44.44 % View solutionQ 12. The price of rice falls by 15 %. By what percentage a person can increase the consumption of rice so that his overall budget does not change? a. 10.74 % b. 17.64 % c. 20.46 % d. 21.90 % View solution
|
|
Type 5: Numericals based on Marks of students In an examination, P scored 30 % marks and failed by 15 marks. Q scored 40 % marks and obtained 35 marks more than those required to pass. Find the pass percentage. a. 30 % b. 33 % c. 35 % d. 40 % View solution Correct Option: (b)
We have to calculate the pass percentage.
In case of P: He scores 30 % out of total marks, but fails by 15 marks. Hence, the simple equation formed is (30 % of x) + 15
In case of Q: He scores 40 % out of total marks, but gets 35 marks more than required to pass. Hence, the simple equation formed is (40 % of x) – 35
1) First calculate total marks.
Let total marks be x.
(30 % of x) + 15 = (40 % of x) – 35 | 30 | × x + 15 = | 40 | × x – 35 | | 100 | 100 |
| 35 + 15 = | 40 | × x – | 30 | × x | | 100 | 100 |
x=500 Total marks = 500 2) As we know the total marks, we can calculate the passing. | Passing Marks = | 30 | × x + 15 | | 100 |
| Passing Marks = | 30 | × 500 + 15 = 165 | | 100 |
Therefore, | Passing Percentage = | 165 | × 100 = 33% | | 500 |
Required pass percentage = 33 % In a science examination, the average obtained by entire class was 80 marks. If 10 % of students scored 92 marks and 20 % of students scored 90 marks, then what was the average of remaining students? a. 65.32 b. 70.56 c. 75.43 d. 77.96 View solution Correct Option: (c)
Here, we do not know the number of students in the class. So let the number of students be 100 and the required average is y.
1) 10 % of students scored 92 marks
2) 20 % of students scored 90 marks
3) Therefore, from 100 students, the remaining students are 70
4) Average obtained by 100 students = 80 marks
Considering the given parameters, form the equation.
(10 x 92) + (20 x 90) + (70 x y) = (100 x 80)
70 y = 8000 – (1800 + 920)
y = 75.43
The average of remaining students = 75.43 A student attempts x number of questions. He answers 15 correctly out of first 20 questions and of the remaining questions, he answers 1/3 correctly. If all questions have same credit and the student gets 50 % marks, then find the value of x. a. 30 b. 35 c. 45 d. 50 View solution Correct Option: (d)
Given:
1) Student attempts x questions.
2) Out of 20 questions he answers 15 correctly and of (x – 20) questions he answered 1/3 correctly.
3) The student gets 50 % marks.
Therefore, | 15 + | 1 | (x – 20) = 50% of x | | 3 |
| 15 + | 1 | (x – 20) = | 50 | × x | | 3 | 100 |
90+2 (x-20)=3x Solving this equation, we get x=50 Hence, the number of question attempted by the students = 50
|
Profit and Loss - Aptitude test, questions, shortcuts, solved example videosProfit and Loss - Quantitative aptitude tutorial with easy tricks, tips, short cuts explaining the concepts. Online aptitude preparation material with practice question bank, examples, solutions and explanations. Video lectures to prepare quantitative aptitude for placement tests and competitive exams like MBA, Bank exams, RBI, IBPS, SSC, SBI, RRB, Railway, LIC, MAT. Very useful for freshers, engineers, software developers taking entrance exams. Learn and take practice tests!
Average - Aptitude test, questions, shortcuts, solved example videosAverage - Quantitative aptitude tutorial with easy tricks, tips, short cuts explaining the concepts. Online aptitude preparation material with practice question bank, examples, solutions and explanations. Video lectures to prepare quantitative aptitude for placement tests and competitive exams like MBA, Bank exams, RBI, IBPS, SSC, SBI, RRB, Railway, LIC, MAT. Very useful for freshers, engineers, software developers taking entrance exams. Learn and take practice tests!
Problem on Ages - Aptitude test, questions, shortcuts, solved example videosProblems on Ages - Quantitative aptitude tutorial with easy tricks, tips, short cuts explaining the concepts. Online aptitude preparation material with practice question bank, examples, solutions and explanations. Video lectures to prepare quantitative aptitude for placement tests and competitive exams like MBA, Bank exams, RBI, IBPS, SSC, SBI, RRB, Railway, LIC, MAT. Very useful for freshers, engineers, software developers taking entrance exams. Learn and take practice tests!