Video on Simplification - shortcuts, tips and tricksSimplifications
Simplification is a chapter which depends on the following chapters. Hence, when dealing with simplifications u must remember all basic concepts and tricks used to solve these numerical on simplification.
1) Numbers
2) H.C.F. and L.C.M.
3) Decimal fractions
4) Square and cube roots
5) Surds and indices
Important points to Remember: 1) This chapter is very important because numerical on simplification are based on concepts related decimal fraction, square and cube roots, H.C.F. and L.C.M., numbers, etc.
2) How to find H.C.F. and L.C.M.
3) Tricks to solve decimal fractions
4) Number system, types of numbers
5) How to find square root and cube root
Basic Formulae: (Must Remember) 1) (a - b)
2 = (a
2 + b
2 - 2ab)
2) (a + b)
2 = (a
2 + b
2 + 2ab)
3) (a + b) (a – b) = (a
2 – b
2 )
4) (a
3 + b
3) = (a + b) (a
2 – ab + b
2)
5) (a
3 - b
3) = (a - b) (a
2 – ab + b
2)
6) (a + b + c)
2 = a
2 + b
2 + c
2 + 2 (ab + bc + ca)
7) (a
3 + b
3 + c
3 – 3abc) = (a + b + c) (a
r>2 + b
2 + c
2 – ab – bc – ac)
Quick Tips and Tricks1) Virnaculum (Bar ‘¬¬–’): If a given expression contains a virnaculum (bar), then first simplify the given expression under virnaculum and then follow the rule of
‘BODMAS’. Step1: When simplifying the given expressions, first brackets are to be removed in the order:
‘––’, ‘( )’, ‘{ }’, ‘[ ]’Step2: The operations are to be performed strictly in the order:
Division, Multiplication, Addition and Subtraction 2) ‘BODMAS Rule’: This rule is used to solve and find out the value of given expressions by performing the operations in a correct sequence.
BODMAS is the shortcut used to remember the procedure of simplification.
B: Bracket
O: Order (i.e. power, square root etc.)
D: Division (Left to right)
M: Multiplication (Left to right)
A: Addition (Left to right)
S: Subtraction (Left to right)
Step1: When simplifying the given expressions, first brackets are to be removed in the order:
( ), { }, [ ] Step2: The operations are to be performed strictly in the order:
Division, Multiplication, Addition and Subtraction 3) Modulus of a real numberThe modulus of a real number or the absolute value is defined as follows:
Modulus of x is written as |x|
| |x| = | 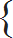 | x, if x > 0 |
| – x, if x < 0 |
Question VarietyQ 1. Simplify: y – [y – (x + y) – {y –(y –
x – y )} + 2x]
a. 0
b. x
c. 4x
d. x/2
View solution Correct Option: (c)
Follow the rule of ‘VBODMAS’
Step 1: Solve the expression below bar
y-[y-(x+y)-{y-(y-x+y) }+2x]
Step 2: Solve () bracket
y-[y-(x+y)-{y-(2y-x) }+2x]
y-[-x-{y-2y+x}+2x]
Step 2: Solve {} bracket
y-[-x-{y-2y+x+2x}]
y-[-x-{-y+3x}]
y-[-x+y-3x]
Step 3: Solve [ ] bracket
y+4x-y
4x
Therefore, correct answer is 4x i.e option (c)
Simplify: 13.05 × 4.5 ÷ 0.5
a. 117.45
b. 112.32
c. 115.50
d. 120.60
View solution Correct Option: (a)
Follow the rule of ‘VBODMAS’
No bar, No bracket. Hence, first step starts from ‘DMAS’
Step 1: Divide 4.5 ÷ 0.5=9
Step 2: Multiply 13.05 × 9 = 117.45
| Q 3. Simplify: 10 – | 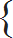 | 5 | 1 | – | 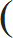 | 7 | 1 | + 2.8 ÷ x | 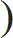 | 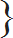 | × 4.25 ÷ (0.2)2 = 306 |
| 2 | 2 |
a. 1.963
b. 2.847
c. 3.562
d. 4.963
View solution