Video on Time and Distance - shortcuts, tips and tricksTime and Distance
Time & Distance is one of the most important chapters for any entrance exam. The concepts of this chapter help you in dealing effectively with the other two chapters i.e
“Trains” and “Boats & Streams”.Important Points to Remember 1) Speed is defined as the distance travelled per unit time.
2) If same distance X is travelled at two different speeds S
1 & S
2, then average speed is calculated by,
| Average Speed (Sa) = | (2S1S2) |
| (S1 + S2) |
3) Two bodies A and B move between two points P & Q. One starts from P and goes to Q while the other starts from Q and goes to P. They meet on the way and reach their destinations in time t
a and t
b respectively after meeting . Their speeds S
a & S
b are given by,
| Sa | = | 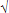 tb tb |
| Sb | 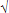 ta ta |
4) When two bodies move in
opposite direction, their
speeds are added to find the relative speed.
SR = S1 + S25) When two bodies move in
same direction, their
speeds are subtracted to find the relative speed.
SR = S1 – S2Conversion of UnitsIt is extremely important to pay attention to the units for each of the quantities given. At times, you may be required to convert the unit of speed from km per hr to metre per second or vice versa.
Converting km/hr into m/s| km | = | 1000 m | = | 5 | m/s |
| hr | 60 x 60 sec | 18 |
Example:
| 20 | km | = 20 x | 5 | = 5.55 m/sec |
| hr | 18 |
Converting m/s into km/hr:Example:
| 20 | m | = 20 x | 18 | = 72 km/hr |
| s | 5 |
- To convert minutes into seconds, multiply by 60
- To convert hours into seconds, multiply by 60 x 60
Question VarietyBasically there are 4 types of questions that are asked from this chapter. Understanding and practicing each of the 4 types will help you deal successfully with the problems from this chapter.Type 1: Calculate either time, speed or distance from the other two given parameters.
How many seconds does Puja take to cover a distance of 500 m, if she runs at a speed of 30 km/hr?
a) 60 sec
b) 82 sec
c) 95 sec
d) 100 sec
View solutionCorrect answer: (a)
Hint:
We see that the distance is given in
metres while the speed is given in
km/hr and the answer is asked in seconds.
| So, convert km/hr into m/s by multiplying | 5 | m/s to the given value of speed. |
| 18 |
| 30 | km | = 30 x | 5 | = | 75 | m/sec |
| hr |
18 | 9 |
i.e. Place these values in the formula:
| Time = 500 x | 9 | = 60 sec |
| 75 |
A cyclist covers a distance of 800 meter in 4 minutes 20 seconds. What is the speed in km/hr of the cyclist?
a) 6.2 km/h
b) 8.4 km/hr
c) 11.05 km/hr
d) 16.07 km/hr
View solutionCorrect answer: (c)
Hint: Convert minutes into secondsTime=4 min 20 sec =260 sec
| Speed = | 800 | = 3.07 m/sec |
| 260 |
Convert the speed from m/s to km/hr by multiplying with (5/18)| 3.07 x | 18 | km/hr = 11.05 km/hr |
| 5 |
A man walking at the rate of 6 km/hr crosses a bridge in 15 minutes. The length of the bridge is ______.
a. 1000 m
b. 1250 m
c. 1500 m
d. 1800 m
View solutionCorrect answer: (c)
Hint: To find the answer in meter, we will first convert distance from km/hour to meter/sec by multiplying it with 5/18 .Also, change 15 minutes to seconds by multiplying it with 60.
Distance = Speed x Time
1. Convert speed into m/sec:
2. Convert time from minutes into seconds = 15 x 60 s = 900 sec
3. Calculate : Distance = 1.66 x 900 = 1500 m