Problems on Trains - Aptitude test, questions, shortcuts, solved example videos

  • Online aptitude test >> Problems on Trains - Aptitude test, questions, shortcuts, solved example videos
Video on Problems on Trains - shortcuts, tips and tricks

Problems on Trains

While studying the chapter “Trains”, we are required to deal with following scenarios:

1. Two trains moving in opposite direction.
2. Two trains moving in same direction.
3. A train crossing a stationary object of a given length like a platform or bridge.
4. A train crossing a stationary object like a pole or a man which can be considered as a point object.

Important Points to Remember

1) If the length of one train is P and the length of second train is Q, the total distance to be covered is (P+Q)

2) Finding Relative speed:


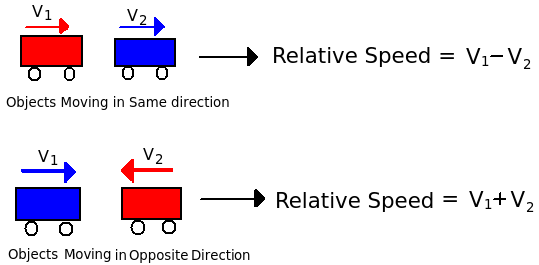
3) If two trains of lengths P and Q move in opposite directions at V1 m/s and V2 m/s, then time taken by the trains to cross each other, can be calculated by
Time Taken = (P + Q)
(V1 + V2)

4) If two trains of different lengths P and Q move in same direction at V1 m/s and V2 m/s, then time taken by the trains to cross each other, is calculated by
Time Taken = (P + Q)
(V1 – V2)

Quick Tips and Tricks

1) Time taken by a train of length L meter to pass a signal post or standing man = Time taken by the train to cover L meter.
Time = L
Speed
A signal post or a standing man is considered to be the point object.

2) The time taken by a train of length L1 meter to pass a stationary object of length L2 is basically the time taken by the train to cover (L1 + L2) meter.
Time = (L1 + L2)
Speed

3) The time taken by a train of length L1 meter to pass a moving object of length L2 is determined by considering the relative speed between the moving objects.
Time = (L1 + L2)
Rs
Rs is the relative speed between moving objects in same or opposite direction.
L1 is the length of train.
L2 is the length of moving object other than train.

4) Two trains start from two points P and Q at the same time and move towards each other. These trains take p and q seconds to reach points Q and P respectively, the relation between them is given by

(P's Speed) = q
(Q's Speed)p

Conversion of Units

1) To convert km/hr into m/s
km = 1000 m = 5m/s
hr60 x 60 sec18
Example: 50 km/hr = 50 x 5 /18 = 13.88 m/s

2) To convert m/s into km/hr
m = 18 km/hr
s5
Example: 50 m/s = 50 x 18 / 5 = 180 km/hr

3) To convert minutes into seconds, multiply by 60

4) To convert hours into seconds, multiply by 60 x 60

The most important thing to remember in this chapter is to ensure the right usage of units and convert them wherever required.

Question Variety

There are 6 types of questions asked from this chapter.

Type 1 : I) A train crosses a stationary object on the platform. Find
a) the time taken or
b) length of train


Examples

Q 1. A train of length 250 m runs at a speed of 70 km/hr. What will be the time taken to cross any stationary object standing at the railway station?

a. 20 sec
b. 17.23 sec
c. 12.86 sec
d. 9.5 sec
View solution

Correct option: (c)

Given: Length of train = 250 m, speed of train = 70 km/hr

Length of train is always considered as distance, and hence here distance = 250 m

1) First convert speed of km/hr into m/s

Speed of train = 70 x 5= 19.44 m/s
18

2) We know that,
Speed = Distance
Time
Time taken to cross stationary object = 250
19.44

Time taken to cross stationary object= 12.86 sec


Q 2. A train takes 10 sec to pass a signal post and covers a distance of 10 km in 15 min. Find the length of train?

a. 100.1 m
b. 223.1 m
c. 111.1 m
d. 120.3 m
View solution

Correct option (c)

We know,

Speed = Distance
Time
Speed = 10 x 60 = 40 x 5 m/sec = 11.1 m/sec
1518

Length of train = (Speed x Time)

= (11.11 x 10)

= 111.1 m

Type 2 : I) A train of given length crosses the platform at a given speed. Find:
a) Time taken to cross the platform or
b) Length of platform


In this type of numerical, the time taken by a train of length L1 meter to pass a stationary object of length L2 is basically the time taken by the train to cover (L1 + L2) meter.
Speed = (L1 + L2)
Time

Examples:

Q 3. Chandigarh express of 100 m runs at a speed of 60 km/hr. What will be the time taken to cross a platform of 150 meters long?

a. 11.00 sec
b. 12.50 sec
c. 15.00 sec
d. 15.23 sec
View solution

Correct option: (c)

Given: Length of train = 100 m, speed of train = 60 km/hr, length of platform = 150 m

1) Always remember first step is the conversion of units.

Convert 60 km/hr into m/s by multiplying it with (5/18)

Speed of the train = 60 x 5 = 16.66 m/s
18

2) Distance covered by the train in passing the platform = (Length of train + Length of platform) = (100 + 150) = 250 m

Therefore,
The time taken = Distance
Speed
= 250
16.66

= 15 sec


Q 4. A train running at 50 km/hr, passes a man walking on the platform at 7 km/hr in same direction as that of train in 15 sec. If this train takes 30 seconds to cross the platform then find the length of train (L1) and length of platform (L2)?

a. L1 =179.1 m, L2 = 237.3 m
b. L1 = 150.5 m, L2 = 300 m
c. L1 = 237.3 m, L2 = 179.1 m
d. L1 = 300 m, L2 = 150.5 m
View solution

Correct option: (a)

Given: Speed of train = 50 km/hr, time required to cross the platform = 30 sec, time required to cross man standing on platform = 15 sec.

1) Convert km/hr into m/s

- 50 km/hr = 50 x 5 = 13.88 m/s
18
- 7 km/hr = 7 x 5 = 1.94 m/s
18

2) The speed of train relative to man = ( 13.88 – 1.94) = 11.94 m/s ---- (The values are subtracted because the train and man move in same direction)

3) Length of train = (Relative speed x Time)

= (11.94) x (15) = 179.1 m

We know,
Speed = (L1 + L2)
Time
13.88 = (L1 + L2)---- consider L1 as length of train and L2 as length of platform
30

(L1 + L2) = 416. 4

L2 = 416.4 – 179.1 = 237.3 m

Type 3: Find time taken by a train to cross a person running in opposite direction at a given speed.


In this type of numerical, generally two values of speeds are mentioned, one is the speed of train and the other is the speed of an object or person. The speed values of train and the moving object are added if they are moving in the direction opposite to each other.

Examples:

Q 5. The Chennai Express of 200 m runs at a speed of 62 km/hr and a person runs on the platform at a speed of 20 km/hr in the direction opposite to that of train. Find the time taken by the train to cross the running person?

a. 8.77 sec
b. 9.77 sec
c. 12.77 sec
d. 13.00 sec
View solution

Correct option: (a)

Given: Length of train = 200 m, speed of train = 62 km/hr, speed of person = 20 km/hr

1) Convert km/hr into m/s

- 62 km/hr = 62 x 5 = 17.22 m/s
18
- 20 km/hr = 20 x 5 = 5.55 m/s
18

As the train and the running person move in opposite directions, their speed values are added to find the relative speed.

Relative speed (Speed of train relative to man) = 17.22 + 5.55 = 22.77 m/s

We know,
Speed = Distance
Time

Therefore, time taken by the train to cross the running person = Time taken by the train to cover 200 m at a relative of 22.77 m/s
= 200 = 8.77 sec
22.78


Q 6. A boy runs opposite to that of train at a speed of 20 km/hr. If the relative speed between train and the boy running in opposite direction is 50 km/hr. What is the length of train, if it takes 20 seconds to cross the boy, when he is at rest?

a. 159.1 m
b. 160.23 m
c. 166.6 m
d. 154.12 m
View solution

Correct option: (c)

Speed = Distance
Time

Relative speed = Speed of train + Speed of boy

50 = Speed of train + 20

Speed of train = 50 – 20 = 30 km/hr

Convert km/hr into m/s
30 km/hr = 30 x 5 = 8.33 m/s
18

Distance = Speed x Time

= 8.33 x 20 = 166.6 m

Type 4: Find time taken by a train to cross a person running in same direction at a given speed.


In this type of numerical, generally two values of speeds are mentioned, one is the speed of train and the other is the speed of an object or person. The speed values of train and the moving object are subtracted if they are moving in same direction.

Examples:

Q 7. A boy runs on the platform of 180 m at a speed of 10 km/hr in the same direction of the train. Find the time taken by the train to cross the running boy if speed of the train is 71 km/hr? (Length of train = Length of platform)

a. 10 sec
b. 10.61 sec
c. 11.23 sec
d. 12 sec
View solution

Correct option: (b)

Given:

Convert km/hr into m/s

- 71 km/hr = 71 x 5 = 19.72 m/s
18
- 20 km/hr = 10 x 5 = 2.77 m/s
18

As the train and the running person move in same direction, their speed values are subtracted to find the relative speed.

Relative speed (Speed of train relative to man) = 19.72 – 2.77 = 16.95 m/s

We know,
Speed = Distance
Time

Therefore, time taken by the train to cross the running person = Time taken by the train to cover 180 m at a relative of 16.95 m/s
= 180 = 10.61 sec
16.95


Q 8. A person is walking at a speed of 5 km/hr along a railway track. If he is 200 m ahead of the train which is 100 m long and runs at a speed of 60 km/hr in same direction, then what is the time required to pass the person?

a. 19.64 sec
b. 15.19 sec
c. 3.2 min
d. 5 min
View solution

Correct option: (a)

Given: Speed of the person = 5 km/hr, length of train = 100 m, speed of train = 60 km/hr

Speed of train relative to walking person = (60 – 5) = 55 km/hr

Convert km/hr into m/s

55 km/hr = 55 x 5 = 15.27 m/s
18

Distance to be covered by the train = 200 + 100 = 300 m

Therefore, time taken by the train to cross the person
= Distance over speed = 300= 19.64 sec
16.27

Type 5: Find time taken by two trains moving in opposite direction at given speed, to cross each other


In this type of numerical, speeds and lengths of trains are correspondingly added because the trains move in opposite direction.

Q 9. Two trains A and B of 150 m and 300 m, run at speed of 65 km/hr and 80 km/hr respectively, in the direction opposite direction to each other. Find the time required to cross each other after the moment they met?

a. 10 sec
b. 11.17 sec
c. 12.30 sec
d. 13.11 sec
View solution

Correct option: (b)

Given:
Length of train A = 150 m, speed = 65 km/hr
Length of train B = 300 m, speed = 80 km/hr

1) Convert km/hr into m/s

65 km/hr = 65 x 5 = 18.05 m/s
18
80 km/hr = 80 x 5 = 22.22 m/s
18

2) As both trains move opposite to each other, relative speed = 18.05 + 22.22 = 40.27 m/s

Distance = (Length of train A + Length of train B) = (150 + 300) = 450 m

We know,
Time = Distance
Speed

Therefore,
Time = 450 = 11.17 sec
40.27 sec

Alternately, we can directly use the formula:
Time = (P + Q) sec
(V1 + V2)
(here P and Q are length of trains and V1 and V2 are speeds of two trains)


Q 10. A passenger train of 200 m runs at a speed of 55 km/hr. A person traveling in it observes that the goods train moving in opposite direction takes 10 seconds to cross him. Find the speed of the goods train, if it is 250 m long.

a. 30.23 km/hr
b. 29.73 km/hr
c. 42.11 km/hr
d. 55 km/hr
View solution

Correct option: (b)

Given: Speed of passenger train = 55 km/hr, length of goods train (P)= 250 , length of passenger train (Q)= 200m

Hint:

Time = (P + Q) sec
(V1 + V2)

Goods train and the passenger train move in opposite direction. Hence, the relative speed is the addition of two speeds.

Convert 55 km/hr into m/s

55 x (5/18) = 15.277 m/s

Therefore,
10 = (250 + 200)
(15.27 + V2)
V2 = 29.73 m/s

Type 6: Two trains move at a given speed in same direction. Find:
a) Time taken to cross each other
b) Length of train


In this type of numerical, lengths of trains are added and speeds are subtracted because the trains move in same direction.

Examples:

Q 11. Two trains P and Q move in same direction with a speed of 85 km/hr and 70 km/hr respectively. If train P is 120 m long and train Q is 240 m, then find taken by train P to cross the train Q?

a. 24 sec
b. 48 sec
c. 84.5 sec
d. 86.5 sec
View solution

Correct option: (d)

Given:
Speed of train P = 70 km/hr, length of train = 120 m
Speed of train Q = 85 km/hr, length of train = 240 m

1) As both trains move in same direction, relative speed = (Speed of train P – Speed of train Q) = (85 – 70) = 15 km/hr

15 km/hr = 15 x5 = 4.16 m/s
18

Distance = 120 +240 = 360 m
Time = Distance
Speed

Time = 360 / 4.16 = 86.5 sec

2) Alternately, we can directly use the formula:
Time = (P + Q)sec
(V1 – V2)
(here P and Q are length of trains and V1 and V2 are speeds of two trains)


Q 12. Two trains moving in same direction run at a speed of 60 km/hr and 40 km/hr respectively. If a man sitting in slow train is passed by the fast train in 10 seconds, then what is the length of the faster train?
a. 53.2 m
b. 55.6 m
c. 150 m
d. 200 m
View solution

Correct option: (b)

Given: Speed of slow train = 60 km/hr, speed of fast train = 40 km/hr

Here both the trains move in same direction. Hence their relative speed is obtained by subtracting the individual speeds of trains.

Relative speed = 60 – 40 = 20 km/hr

1) Convert km/hr into m/s

20 x 5 = 100 = 5.56 m/s
1818

2) Distance (Length of faster train) = Speed x Time

Length of faster train = 5.56 x 10 m = 55.6 m
Time and Distance - Aptitude test, questions, shortcuts, solved example videos
Time and Distance - Quantitative aptitude tutorial with easy tricks, tips, short cuts explaining the concepts. Online aptitude preparation material with practice question bank, examples, solutions and explanations. Video lectures to prepare quantitative aptitude for placement tests and competitive exams like MBA, Bank exams, RBI, IBPS, SSC, SBI, RRB, Railway, LIC, MAT. Very useful for freshers, engineers, software developers taking entrance exams. Learn and take practice tests!
Time and Work - Aptitude test, questions, shortcuts, solved example videos
Time and Work - Quantitative aptitude tutorial with easy tricks, tips, short cuts explaining the concepts. Online aptitude preparation material with practice question bank, examples, solutions and explanations. Video lectures to prepare quantitative aptitude for placement tests and competitive exams like MBA, Bank exams, RBI, IBPS, SSC, SBI, RRB, Railway, LIC, MAT. Very useful for freshers, engineers, software developers taking entrance exams. Learn and take practice tests!
Simple Interest - Aptitude test, questions, shortcuts, solved example videos
Simple Interest - Quantitative aptitude tutorial with easy tricks, tips, short cuts explaining the concepts. Online aptitude preparation material with practice question bank, examples, solutions and explanations. Video lectures to prepare quantitative aptitude for placement tests and competitive exams like MBA, Bank exams, RBI, IBPS, SSC, SBI, RRB, Railway, LIC, MAT. Very useful for freshers, engineers, software developers taking entrance exams. Learn and take practice tests!
Post your comment
Discussion Board
question no 12
there is a mistake that, the speed of slow train is 40 and 60 for fast.
Gokulraaju 03-23-2021
Question no 10
change option km/hr to m/sec.
Koli Shrikant Suresh 06-21-2020
Question no 10
change option km/hr to m/sec.
Koli Shrikant Suresh 06-21-2020
miskate
there are a lots of number mistake in all the question set
Akshay Waghmare 12-20-2019

Related Content

Follow us

▲