Algorithm questions and answers

Algorithm questions and answers

(1) Starting from the root and performing ____________, level order traversal of a rooted tree can be done.

(A) Breadth first search
(B) Depth first search
(C) In-order traversal
(D) Pre-order traversal

View Answer / Hide Answer


(2) We have a hash function and a hash table. The size of hash table is 7 with starting index zero. The hash function is (3x+4) mod 7. Assume that initially the hash table is empty and the sequence 1, 3, 8, 10 is inserted into the table using closed hashing. The content of the table is (‘_’ denotes an empty location in the table)

(A) 1, _, _, _, _, _, 3
(B) 8, _, _, _, _, _, 10
(C) 1, 8, 10, _, _, _, 3
(D) 1, 10, 8, _, _, _, 3

View Answer / Hide Answer


(3) Which one of the following statement is false if G is an undirected graph with distinct edge weight, Emax is the edge with maximum weight and Emin is the edge with minimum weight?

(A) Emin is present in every minimum spanning tree of G
(B) Emax is not present in any minimum spanning tree.
(C) The removal of Emax must disconnect G, if Emax is in a minimum spanning tree.
(D) G has a unique minimum spanning tree.

View Answer / Hide Answer


(4) Consider an array L. If an element in an array L is greater than all elements to the right of it then it is called a leader. The best algorithm to find all leaders in an array

(A) Solves it in time θ (n^²)
(B) Solves it in linear time using a left to right pass of the array
(C) Solves it in linear time using a right to left pass of the array
(D) Solves it using divide and conquer in time θ (n logn)

View Answer / Hide Answer


For questions 5 and 6 refer to the data given below:

Table shows the tasks Ti to be completed and the profit Pi that can be earned if the task is completed before the end of the deadline di th unit of time. The execution of each task requires

one unit and at a time only one task can be executed.



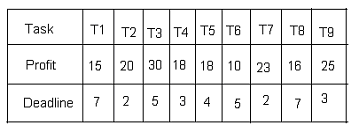(5) Which one of the following statement is true?

(A) All tasks are completed in the schedule time that gives maximum profit.
(B) T4 and T6 are left out
(C) T1 and T8 are left out
(D) T1 and T6 are left out

View Answer / Hide Answer


(6) The maximum profit that can be earned is

(A) 165
(B) 147
(C) 167
(D) 175

View Answer / Hide Answer


(7) Consider a complete n-array tree. This tree is such that each node has either n number of children or no children. Let l = 10 be the number of internal nodes and L = 41 be the number

of leaves in a complete n-array tree. The value of n is

(A) 5
(B) 4
(C) 3
(D) 2

View Answer / Hide Answer


For Questions 8 and 9 refer to the data given below:

int f1(int n)
{
if (n == 0 II n == 1)
return n;
else
return (2*f1(n-1) + 3*f1(n-2));
}

int f2(int n)
{
int a;
int X[N], Y[N], Z[N];
X[0] = Y[0] = Z[0] = 0;
X[1] = 1;
Y[1] = 2;
Z[1] = 3;
for(a = 2; a<=n; a++)
{
X[a] = Y[a-1] + Z[a-2];
Y[a] = 2*X[a];
Z[a] = 3*X[a];
}
return X[n];
}

(8) What is the running time of f1(n) and f2(n) respectively?

(A) θ (2ⁿ) and θ (2ⁿ)
(B) θ (n) and θ (2ⁿ)
(C) θ (2ⁿ) and θ(n)
(D) θ (n) and θ (n)

View Answer / Hide Answer


(9) What is the return value of f1(8) and f2(8) respectively?

(A) 1661 and 1640
(B) 1640 and 1661
(C) 59 and 59
(D) 1640 and 1640

View Answer / Hide Answer


(10) Let i, j and n be the integer variables of the C program fragment given below.

For (i = n, j = 0; i > 0; i /=2, j += i). After termination of the for loop the value stored in the variable j is denoted by val (j). The statement, which is true for this, is

(A) val (j) = θ (n/2)
(B) val (j) = θ (log n)
(C) val (j) = θ (2n)
(D) val (j) = θ (n)

View Answer / Hide Answer


(11) In a complete binary tree, LASTPOST denotes the last vertex visited in a post order traversal, LASTIN denotes the last vertex visited in an inorder traversal and LASTPRE denotes the last vertex visited in a preorder traversal. The statement, which always holds true, is

(A) LASTIN = LASTPRE
(B) LASTPRE = LASTPOST
(C) LASTIN = LASTPOST
(D) None of the above.

View Answer / Hide Answer


(12) For the graph shown below the number of articulation points is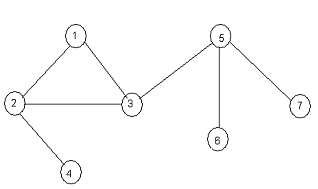



(A) 3
(B) 2
(C) 1
(D) 0

View Answer / Hide Answer


(13) Which one of the following statement is false?

(A) √ logn = O (log log n)
(B) 100n log n = O (nlogn/100)
(C) 2n ≠ O (nk)
(D) If 0x = O (n^y)

View Answer / Hide Answer

ANSWER: 2n ≠ O (nk)

(14) Consider an unweighted, undirected connected graph. In terms of time complexity, the shortest path from a node S to every other node is most efficiently computed by

(A) Performing a DFS starting from S
(B) Performing a BFS starting from S
(C) Warshall’s algorithm
(D) Dijkstra’s algorithm starting from S

View Answer / Hide Answer

ANSWER: Performing a BFS starting from S

(15) _____________ in place sorting algorithm needs the minimum number of swaps.

(A) Selection sort
(B) Quick sort
(C) Insertion sort
(D) Heap sort

View Answer / Hide Answer

ANSWER: Selection sort

(16) The algorithm is as given below:

Procedure A(n)
If n<=2
Return (1)
Else
Return (A( √n));
The running time of this algorithm is best described by

(A) O(log n)
(B) O(n)
(C) O(log log n)
(D) O(1)

View Answer / Hide Answer

ANSWER: O(n)

(17) Consider an undirected graph G whose depth first search tree is T and vertices u and v are the leaves of this tree. The degrees of both u and v in G are at least 2. The statement that holds true is

(A) There must exist a vertex whose removal disconnects u and v in G
(B) There must exist a vertex adjacent to both u and v in G
(C) There must exist a cycle in G containing u and all its neighbours in G
(D) There must exist a cycle in G containing u and v

View Answer / Hide Answer

ANSWER: There must exist a cycle in G containing u and all its neighbours in G

(18) _____________ is used if the concatenation of two lists is to be performed on O(1) time?

(A) Array implementation of list
(B) Circular doubly linked list
(C) Singly linked list
(D) Doubly linked list

View Answer / Hide Answer

ANSWER: Circular doubly linked list

(19) The vertices of a cycle with n nodes is to be coloured in such a way that no two adjacent nodes have the same colour. The minimum number of colours required is

(A) n!
(B) 3
(C) n - 2 n/2 +2
(D) 2

View Answer / Hide Answer

ANSWER: n - 2 n/2 +2

(20) A set V = {v1, v2,…., vn} has n number of vertices. Out of this given set, the number of undirected graphs (not necessarily connected) that can be constructed are

(A) 2^n(n-1)/2
(B) n
(C) n!
(D) None of the above

View Answer / Hide Answer

ANSWER: 2^n(n-1)/2

(21) Which data structure is to be used to implement Dijkstra’s shortest path algorithm on unweighted graphs so that runs in linear time?

(A) Stack
(B) Heap
(C) Queue
(D) B-Tree

View Answer / Hide Answer

ANSWER: Heap

(22) Which one of the following option is true for merge sort?

(A) It uses greedy approach
(B) It uses heuristic search
(C) It uses divide and conquer strategy
(D) It uses backtracking approach

View Answer / Hide Answer

ANSWER: It uses divide and conquer strategy

(23) Match the following:

List I List II

u) All pairs shortest paths p) Greedy
v) Quick sort q) Depth first search
w) Minimum weight spanning tree r) Dynamic programming
x) Connected components s) Divide and conquer

(A) u – r, v – s, w – p, x - q
(B) u – r, v – p, w – s, x - q
(C) u – q, v – p, w – r, x - s
(D) u – p, v – s, w – r, x - q

View Answer / Hide Answer

ANSWER: u – r, v – s, w – p, x - q

(24) The recurrence relation capturing the optimal execution time of the towers of Hanoi problem with n discs is

(A) T(n) = 2T(n-2) + 2
(B) T(n) = 2T(n-2) + 1
(C) T(n) = 2T(n-1) + 1
(D) T(n) = 2T(n-1) + 2

View Answer / Hide Answer

ANSWER: T(n) = 2T(n-1) + 1

(25) Consider two positive function of n: f(n) = n^² log n and g(n) = n(log n) ¹⁰. The statement which is correct for these two functions, is

(A) f(n) = O(g(n)) and g(n) = O(f(n))
(B) f(n) ≠ O(g(n)) and g(n) ≠ O(f(n))
(C) f(n) = O(g(n)) and g(n) ≠ O(f(n))
(D) f(n) ≠ O(g(n)) and g(n) = O(f(n))

View Answer / Hide Answer

ANSWER: f(n) ≠ O(g(n)) and g(n) ≠ O(f(n))

For the Questions 26 and 27 refer to the data given below:

The probability of letters a = 1/2, b = 1/4, c = 1/8, d = 1/16, e = 1/32, f = 1/32.

(26) The Huffman code for the letter a, b, c, d, e, f is

(A) 10, 110, 1111, 1010, 1100, 00110
(B) 11, 10, 01, 001, 0001, 0000
(C) 1, 11, 111, 1110, 11000, 10000
(D) 0, 10, 110, 1110, 11110, 11111

View Answer / Hide Answer

ANSWER: 0, 10, 110, 1110, 11110, 11111

(27) The average length of the correct answer to question 26 is

(A) 1.9375
(B) 2.3546
(C) 4
(D) 3.3241

View Answer / Hide Answer

ANSWER: 1.9375

(28) To evaluate polynomial x (j) = m0 + m1j + m2j^² + m3j^³ where mi ≠ 0, the minimum number of multiplications needed on the input j is

(A) 6
(B) 5
(C) 3
(D) 4

View Answer / Hide Answer

ANSWER: 3

(29) Consider the graph shown below. When Dijkstra’s single source shortest path algorithm run from vertex a, it computes the correct shortest path distance to



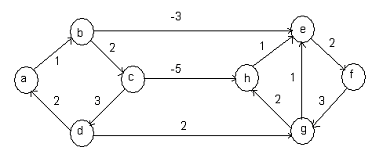
(A) Vertices a, b, c, d
(B) Vertices a, e, f, g, h
(C) Only vertex a
(D) All the vertices

View Answer / Hide Answer

ANSWER: Vertices a, b, c, d

(30) We have two sorted lists whose sizes are a and b. For merging these two lists into a sorted list of size a + b, we require comparisons of

(A) O (log a + log b)
(B) O (a + b)
(C) O (a)
(D) O (b)

View Answer / Hide Answer

ANSWER: O (a + b)

(31) The technique of sorting is called stable if and only if

(A) It uses divide and conquer technique
(B) It takes O (n) space
(C) It takes O (n log n) time
(D) It maintains the relative order of occurrence of non-distinct elements

View Answer / Hide Answer

ANSWER: It maintains the relative order of occurrence of non-distinct elements

(32) What is the maximum number of nodes in a binary tree whose height is h where height is the maximum number of edges in any root to leaf path?

(A) 2^h+1
(B) 2^h+1 - 1
(C) 2^h
(D) 2^h-1

View Answer / Hide Answer

ANSWER: 2^h+1 - 1

For questions 33 and 34 refer to the data given below:

Double func(int n)
{
int j;
double sum;
if(j ==0)
return 1.0;
else
{
sum = 0.0;
for(j = 0; j sum += func(j);
return sum;
}
}

(33) What is the space complexity of the above function?

(A) O(n!)
(B) O(n)
(C) O(n^²)
(D) O(log n)

View Answer / Hide Answer

ANSWER: O(n!)

(34) When the above function func() is modified and store the values of func(j), 0<=j
significantly. What is the space complexity of the modified function?

(A) O(n!)
(B) O(n)
(C) O(n²)
(D) O(log n)

View Answer / Hide Answer

ANSWER: O(n)

(36) Consider a graph G on vertices n and 2n-2 edges. The statement that does not hold true for graph G, when the edges of the graph G is partitioned into two edge-disjoint spanning trees, is

(A) Between every pair of vertex there are two vertex-disjoint paths.
(B) Between every pair of vertex there are two edge-disjoint paths
(C) There are at least two edges for the minimum cut in G.
(D) At most 2k-2 edges are present in the induced subgraph for every subset of k vertices

View Answer / Hide Answer

ANSWER: Between every pair of vertex there are two vertex-disjoint paths.

(37) The implementation of Breadth first search algorithm has been done using queue data structure. In the graph shown below, one possible order of visiting the nodes is



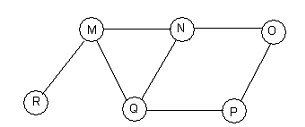
(A) NQMPOR
(B) MNOPQR
(C) QMNPOR
(D) QMNPRO

View Answer / Hide Answer

ANSWER: QMNPRO

(38) Consider a rooted tree with n nodes. Each node is having 0 or 3 children. The number of leaf nodes in the rooted tree is

(A) (n-1)/2
(B) (n-1)/3
(C) (2n + 1)/3
(D) n/2

View Answer / Hide Answer

ANSWER: (2n + 1)/3

(39) T(n) = 2T(n/2) + n and T(0) = T(1) = 1. The statement, which is not true, is

(A) T(n) = θ (n log n)
(B) T(n) = O(n log n)
(C) T(n) = O(n^²)
(D) T(n) = Ω (n^²)

View Answer / Hide Answer

ANSWER: T(n) = θ (n log n)

(40) We have a Max heap, which is represented by an array, and the process of inserting an element into it is going on. How many comparisons are done to find the position for the newly inserted element if we perform a binary search on the path from the new leaf to the root?

(A) θ (log2 n)
(B) θ (log2 log2 n)
(C) θ (log2 n/2)
(D) θ (n)

View Answer / Hide Answer

ANSWER: θ (log2 n)

(41) What is the maximum number of edges in an n-node unidirectional graph without self loops?

(A) n/2
(B) (n + 1)(n)/2
(C) n+1
(D) n(n-1)/2

View Answer / Hide Answer

ANSWER: (n + 1)(n)/2

(42) Which one of the following statement is true for the recurrence T(n) = 2T([√n]) + 1, T(1) = 1?

(A) T(n) = θ (2n)
(B) T(n) = θ (n)
(C) T(n) = θ (log log n)
(D) T(n) = θ (log)

View Answer / Hide Answer

ANSWER: T(n) = θ (log log n)

(43) From the scratch a B-tree of the order of 4 is built by 10 successive iterations. The maximum number of node splitting operations that may take place is

(A) 6
(B) 5
(C) 4
(D) 3

View Answer / Hide Answer

ANSWER: 3

(44) T1 and T2 are the time taken by the Quicksort program P to sort the inputs [1 2 3 4] and [5 4 3 2 1] in ascending order respectively. The statement that holds true is

(A) T1 = T2
(B) T1 < T2
(C) T1 > T2
(D) T1 = T2 + 5 log 5

View Answer / Hide Answer

ANSWER: T1 = T2

(45) To convert the array 8, 19, 40, 17, 12, 10, 2, 5, 7, 11, 6, 9, 70 into a heap with maximum elements at the root, the minimum number of interchanges needed are

(A) 0
(B) 1
(C) 2
(D) 3

View Answer / Hide Answer

ANSWER: 2

(46) Out of 4 distinct keys the number of distinct binary search trees that can be created is

(A) 10
(B) 14
(C) 8
(D) 24

View Answer / Hide Answer

ANSWER: 14

(47) Consider the statements given below and find the correct option regarding Bellman-Ford shortest path algorithm.

I) It always finds a negative weighted cycle, if one exists.
II) It finds whether any negative weighted cycle is reachable from the source.

(A) Only II holds true
(B) Only I holds true
(C) Both I and II holds true
(D) Neither I nor II holds true

View Answer / Hide Answer

ANSWER: Only II holds true

For questions 48 and 49 refer to the data given below:

Consider the matrix W given below where entry Wij is the weight of the edge {i, j}. We have a complete undirected graph with vertex set {0, 1, 2, 3, 4}.



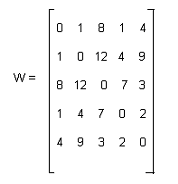
(48) The minimum possible weight of a spanning tree T in this graph such that vertex 0 is a leaf node in the tree T is

(A) 4
(B) 7
(C) 10
(D) 5

View Answer / Hide Answer

ANSWER: 10

(49) The minimum possible weight of a path P from vertex 1 to vertex 2 in this graph such that P contains at most 3 edges is

(A) 9
(B) 8
(C) 7
(D) 6

View Answer / Hide Answer

ANSWER: 8

(50) We have hash function x mod 10 and the following input (4322, 1334, 1471, 9679, 1989, 6171, 6173, 4199). From the statements given below the one, which holds true, is

I. 9679, 1989, 4199 hash to the same value.
II. 1472, 1671 hash to the same value
III. All elements hash to the same value
IV. Each element hashes to a different value.

(A) Only I
(B) I and IV
(C) II and III
(D) I and II

View Answer / Hide Answer

ANSWER: I and II

(51) int func(a, b)
{
if(a%b == 0)
return b;
a = a%b;
return func(b, a);
}

In the above function let a = b. The number of recursive calls made by this function is

(A) θ (log2 n)
(B) θ (log2 log2 n)
(C) θ (log2 n/2)
(D) θ (n)

View Answer / Hide Answer

ANSWER: θ (log2 n)

(52) In the worst-case scenario, the number of swaps required to sort n elements using selection sort is

(A) θ (logn)
(B) θ (n)
(C) θ (n/2)
(D) θ (n^²)

View Answer / Hide Answer

ANSWER: θ (n)

(53) We have the functions as given below:

f(n) = 2ⁿ , g(n) = n! and h(n) = n^{log n}. The statement that holds true about the asymptotic behaviour of functions f(n), g(n) and h(n) is

(A) h(n) = O(f(n)); g(n) = Ω (f(n))
(B) g(n) = O(f(n)); h(n) = O(f(n))
(C) f(n) = O(g(n)); g(n) = O(h(n))
(D) f(n) = Ω (g(n)); g(n) = O(h(n))

View Answer / Hide Answer

ANSWER: h(n) = O(f(n)); g(n) = Ω (f(n))

(54) Matrix M1 is to be stored in array A and matrix M2 is to be stored in array B. Considering each array to be stored either in row-major or column-major order in contiguous memory locations, the time complexity of an algorithm to compute M1xM2 will be

(A) Independent of the storage scheme.
(B) Best if both the array will be in column-major
(C) Best if array A will be in row-major and array B will be in column-major order
(D) Best if both the array will be in row-major

View Answer / Hide Answer

ANSWER: Best if array A will be in row-major and array B will be in column-major order

(55) Two inputs that are to be sorted in ascending order using quicksort are given below:

I) 1, 2, 3 …… n
II) n, n-1, n-2, …… 2, 1

For the inputs given above the number of comparisons that are to be made is represented by C1 and C2. Then,

(A) C1 > C2
(B) C1 = C2
(C) C1 < C2
(D) None of the above

View Answer / Hide Answer

ANSWER: C1 = C2

(56) Consider that each set is represented as a linked list with elements in arbitrary order. Which one of the following operations is the slowest?

(A) Membership and cardinality
(B) Union only
(C) Intersection and membership
(D) Union and intersection

View Answer / Hide Answer

ANSWER: Union and intersection

(57) Consider n number of elements whose median can be found in O(n) time. The statement that is correct about the complexity of quick sort, in which median is selected as a pivot is

(A) θ (n logn)
(B) θ (n^²)
(C) θ (n)
(D) θ (n^³)

View Answer / Hide Answer

ANSWER: θ (n^²)

(58) Package A and package B are the two alternative packages for processing a database that has 10^k records. To process n records package A takes 0.0001n^² time units and package B takes 10nlog10n time units. The smallest value of k for which package B will be preferred over package A is

(A) 6
(B) 10
(C) 2
(D) 5

View Answer / Hide Answer

ANSWER: 6

(59) The graph is as shown below. From the options given below the one, which is not the sequence of edges added to the minimum spanning tree using Kruskal’s algorithm, is



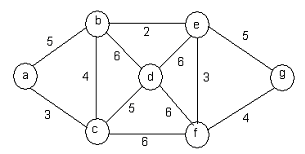
(A) (b, e) (a, c) (e, f) (b, c) (f, g) (c, d)
(B) (b, e) (e, f) (a, c) (b, c) (f, g) (c, d)
(C) (b, e) (e, f) (b, c) (a, c) (f, g) (c, d)
(D) (b, e) (e, f) (a, c) (f, g) (b, c) (c, d)

View Answer / Hide Answer

ANSWER: (b, e) (e, f) (b, c) (a, c) (f, g) (c, d)

(60) The adjacency matrix of an undirected graph G that has n nodes is given by an nxn square matrix whose diagonal and non-diagonal elements are 0’s and 1’s respectively. Graph G has

(A) Unique minimum spanning tree of cost n-1
(B) No minimum spanning tree (MST)
(C) Multiple spanning trees of different costs
(D) Multiple distinct MST’s, each of cost n-1

View Answer / Hide Answer

ANSWER: Multiple distinct MST’s, each of cost n-1