Digital logic test questions for interview, exams, entrance
(1) For the function f (w, x, y, z) = ∑ (0, 4, 5, 7, 8, 9, 13, 15) the expression which is pre not equivalent to f is(A) x’y’z’ + wx’y’ + w’y
(B) xyz + wx’y’ + w’y
(C) x’y’z’ + wy’ + w’yz + wz
(D) x’yz’ + x’y’ + w’y + xz
View Answer / Hide AnswerANSWER: x’y’z’ + wx’y’ + w’y
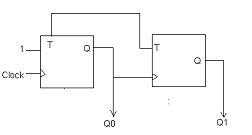
(A) 01, 10, 01, 10
(B) 11, 11, 00, 10
(C) 11, 10, 01, 00
(D) 00, 10, 10, 10
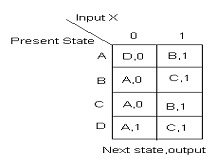
View Answer / Hide Answer(3) The finite state machine shown below takes binary input from the least significant bit. The statement that holds true is 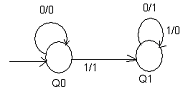
(A) 1’s compliment of the input number is computed
(B) 2’s compliment of the input number is computed
(C) The input number is decremented
(D) The input number is increment
View Answer / Hide AnswerANSWER: 2’s compliment of the input number is computed
In the initial k bits of the input, number of 0’s is represented by zk and number of 1’s is represented by nk.
(zk + nk = k). The output of the circuit is 00 only if one of the conditions given below is correct.
Case 1. zk – nk = 2, the output at the kth and all subsequent clock ticks is 10.
Case 2. nk – zk = 2, the output at the kth and all subsequent clock ticks is 01.
In the state transition graph of the above circuit the minimum number of states required is
(A) 6
(B) 5
(C) 8
(D) 7
View Answer / Hide Answer(5) For the number (-539)10 the 2’s compliment representation in hexadecimal form is(A) DE5
(B) DBC
(C) 9D6
(D) ABC
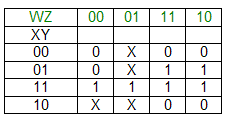
View Answer / Hide Answer(6) Consider the karnaugh map shown below where X denotes “don’t care”. The literal count of a Boolean expression is defined as the sum of the number of times each literal appears in the expression. For example, the literal count of (xy + xz) is 4. The minimum possible literal counts of the POS and SOP representations respectively of the function given by the Karnaugh map is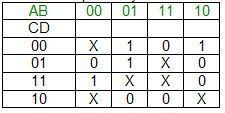
(A) (9, 10)
(B) (10, 9)
(C) (11, 11)
(D) (12, 13)
View Answer / Hide Answer(7) What is the 2’s compliment representation of the number 43?(A) 11000110
(B) 00101011
(C) 01011101
(D) 10010010
View Answer / Hide Answer(8) For the circuit shown below the statement that holds true is 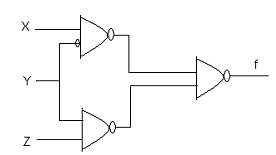
(A) f is independent of X.
(B) f is independent of Y.
(C) f is independent of Z.
(D) None of X, Y, Z is redundant.
View Answer / Hide AnswerANSWER: None of X, Y, Z is redundant.
(A) XY + YW
(B) (W + X)(W + Y)(X + Y)
(C) (W + Y) X
(D) None of the above
View Answer / Hide AnswerANSWER: None of the above
X: = A + B
Y: = A + C
X: = X + C
Y: = Y + B
What is the value of X and Y?(A) X = Y = 0.0
(B) X = 0.0, Y = 1.0
(C) X = 1.0, Y = 0.0
(D) X = Y = 1.0
View Answer / Hide Answer(11) The function that implements karnaugh map shown below is 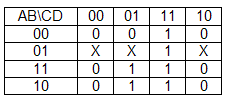
(A) (C + D)(C’ + D)(A + B)
(B) D(C + A)
(C) A’B + CD
(D) AD + A’B
View Answer / Hide Answer(12) What is the minterm expansion of f (P, Q, R) = PQ + QR’ + PR’ ?(A) m2 + m3 + m0 + m6
(B) m2 + m0 + m3 + m1
(C) m2 + m4 + m6 + m1
(D) m0 + m4 + m6 + m1
View Answer / Hide AnswerANSWER: m2 + m4 + m6 + m1
(A) 1
(B) 2
(C) 3
(D) 4
View Answer / Hide Answer(14) For the decimal number –57 Booth’s coding in 8 bits is(A) 0 – 100 + 100 - 1
(B) 0 – 100 + 1000
(C) 00 – 10 +100 - 1
(D) 0 – 1 + 100 - 1
View Answer / Hide AnswerANSWER: 0 – 100 + 100 - 1
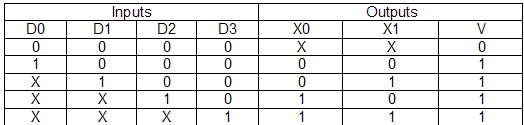
If the input is valid then only V = 1. The truth table represents
(A) Demultiplexer
(B) Multiplexer
(C) Decoder
(D) Priority encoder
View Answer / Hide Answer(16) When the multiplier pattern is ________________ Booth’s algorithm for integer multiplication gives worst performance.(A) 011111……..11110
(B) 101010………1010
(C) 100000…..001
(D) 111111…….1111
View Answer / Hide Answer(17) Zero has two representations in(A) 1’s compliment
(B) Sign magnitude
(C) Both A and B
(D) Neither A nor B
View Answer / Hide Answer(18) The figure shows the arrangement of master slave flip-flops. The initial state of P is 0 and that of Q is 1. The output state P and Q after the clock cycles is respectively 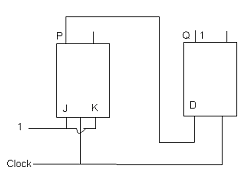
(A) 0, 0
(B) 0, 1
(C) 1, 1
(D) 1, 0
View Answer / Hide Answer(19) To implement any arbitrary Boolean function the set of components that are sufficient is(A) AND gate and NOT gate
(B) AND gate and XOR gate
(C) 2 to 1 multiplexer
(D) XOR gate and NOT gate
View Answer / Hide AnswerANSWER: AND gate and XOR gate
(A) Fraction bits of 100….000 and exponent value of 0
(B) Fraction bits of 000….000 and exponent value of -1
(C) Fraction bits of 000….000 and exponent value of 0
(D) No exact representation
View Answer / Hide AnswerANSWER: Fraction bits of 100….000 and exponent value of 0
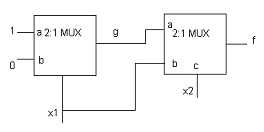
(A) f = x1 + x2
(B) f = x1x2 + x1’x2’
(C) f = x1 + x2’
(D) f = x1’ + x2
View Answer / Hide AnswerANSWER: f = x1x2 + x1’x2’
x + y + z = 1
xy = 0
xz + w = 1
xy + z’w’ = 0
The values of x, y, z and w are respectively
(A) 1 0 1 1
(B) 1 0 0 0
(C) 1 1 0 0
(D) 0 1 1 0
View Answer / Hide Answer(23) What is the simplified expression for the function f (f (x + y, y), z) if f (A, B) = A’ + B?(A) x + y’
(B) x’ + z
(C) xyz
(D) None of the above
View Answer / Hide AnswerANSWER: None of the above
(A) 3 time unit
(B) 15 time unit
(C) 10 time unit
(D) 6 time unit
View Answer / Hide Answer(25) The output of the circuit is in the form of 4-bit. The output 0 is represented by 0000, 1 by 0001… 9 by 1001. If we design a combinational circuit which takes these 4 bits as input the output will be 1 if the digit = 5 and otherwise. Only AND, OR and NOT gates are to be used. To design this circuit the minimum number of gates required is(A) 2
(B) 3
(C) 4
(D) 5
View Answer / Hide Answer(26) Two 8 bit 2’s compliment number’s are 1111 1010 and 0000 1010. Their product in 2’s compliment is(A) 1100 0100
(B) 1010 0010
(C) 1100 1100
(D) 1000 1111
View Answer / Hide Answer(27) For the Boolean function f (a, b, c) = a’c + ac’ + b’c the essential prime implicants are(A) ac’ and bc’
(B) a’c only
(C) a’c and b’c
(D) a’c and ac’
View Answer / Hide Answer(28) Sign extension is a step in(A) Signed 16bit integer addition
(B) Arithmetic left shift
(C) Converting a signed integer from one size to another
(D) Floating point multiplication
View Answer / Hide AnswerANSWER: Floating point multiplication
For questions 29 and 30 refer to the data given below:
The floating-point format is given below whose mantissa is a pure fraction in sign-magnitude form:
 (29) The hexadecimal representation (without normalization and rounding off) of the decimal number 0.239 x 213 is
(29) The hexadecimal representation (without normalization and rounding off) of the decimal number 0.239 x 213 is(A) 4D0D
(B) 4D3D
(C) 0D24
(D) 0D4D
View Answer / Hide Answer(30) For the above format the normalized representation is specified as follows: The mantissa has an implicit preceding the binary (radix) point. Assuming that only 0’s are padded in while shifting a field the normalized representation of the above number 0.239 x
2
13 is
(A) D0D0
(B) 4AE8
(C) 49D0
(D) D048
View Answer / Hide Answer(31) Consider a number n whose 4-bit gray code representation is a3a2a1a0 and the gray code of (n + 1) (module 16) is b3b2b1b0. The function, which is correct, is(A) b3 (a3a2a1a0) = ∑ (0, 1, 6, 7, 10, 13, 14, 15)
(B) b2 (a3a2a1a0) = ∑ (2, 4, 5, 6, 10, 13, 14, 15)
(C) b1 (a3a2a1a0) = ∑ (4, 9, 10, 11, 12, 13, 14, 15)
(D) b0 (a3a2a1a0) = ∑ (1, 2, 3, 6, 10, 13, 14, 15)
View Answer / Hide AnswerANSWER: b1 (a3a2a1a0) = ∑ (4, 9, 10, 11, 12, 13, 14, 15)
(A) 10001
(B) 11100
(C) 11010
(D) 11111
View Answer / Hide Answer(33) We have the Boolean expression X * Y = XY + X’Y’ and Z = X * Y. Which of the following is a valid expression?(A) X = Y * Z
(B) Y = X * Z
(C) X * Y * Z = 1
(D) All of the above
View Answer / Hide Answer(34) What is the minimum size of multiplexer needed to implement any Boolean function of n variables if we are allowed to use only one multiplexer and one inverter?(A) 2
n-2 line to 1 line
(B) 2
n+1 line to 1 line
(C) 2
n line to 1 line
(D) 2
n-1 line to 1 line
View Answer / Hide AnswerANSWER: 2n-1 line to 1 line
(A) It cannot be represented precisely in binary
(B) It is equivalent to binary value 0.001
(C) It is equivalent to binary value 0.01
(D) It is equivalent to binary value 0.1
View Answer / Hide AnswerANSWER: It is equivalent to binary value 0.01
(A) 10, 12
(B) 8, 11
(C) 9, 13
(D) None of the above
View Answer / Hide Answer(37) We have the function with four variables f (A, B, C, D) = ∑ (1, 4, 5, 9, 11, 12). The switching expression corresponding to this function is(A) BC’D’ + A’C’D + AB’D
(B) ABC’ + BCD’ + AB’D
(C) A’B’C’ + A’CD + AC’D’
(D) ACD’ + A’B’C + ABD
View Answer / Hide AnswerANSWER: BC’D’ + A’C’D + AB’D
(113 + - 111) + 7.51
113 + (-111 + 7.51)
The result will be(A) 10.0 and 9.51
(B) 10.0 and 10.0
(C) 9.51 and 10.0
(D) 9.51 and 9.51
View Answer / Hide Answer(39) By cross-coupling two NAND gates an SR latch is made. If the inputs S = R = 0 then the output will be(A) Q = 1, Q’ = 1
(B) Q = 0, Q’ = 1
(C) Q = 1, Q’ = 0
(D) Indeterminate states
View Answer / Hide AnswerANSWER: Indeterminate states
(A) 11011011
(B) 11100111
(C) 11010111
(D) 11100100
View Answer / Hide Answer(41) A Boolean function x’y’ + xy + x’y is equivalent to(A) x’ + y’
(B) x + y’
(C) x’ + y
(D) x + y
View Answer / Hide Answer(42) The function with four variables f (a, b, c, d) = ∑ (1, 3, 4, 6, 9, 11, 12, 14 is(A) Independent of two variables
(B) Independent of one variable
(C) Independent of three variables
(D) Dependent on all the variables
View Answer / Hide AnswerANSWER: Independent of two variables
(A) 108
(B) 32F
(C) D78
(D) 1AF
View Answer / Hide Answer(44) Which one of the following is equivalent to (1217) 8?(A) (1217)
16(B) (2424)
16(C) (028F)
16(D) (0B25)
16View Answer / Hide Answer(45) If we have n number of Boolean variables then the maximum number of different Boolean functions involving n is(A) n
n (B) 2n
(C) n
2 (D) None of the above
View Answer / Hide AnswerANSWER: None of the above
(A) -(2
n-1 -1) to (2
n-1 -1)
(B) -2
n-1 to (2
n-1 –1)
(C) -(2
n-1 +1) to (2
n-1 -1)
(D) -2
n-1 to 2
n-1View Answer / Hide AnswerANSWER: -2n-1 to (2n-1 –1)
(A) The special value +0
(B) The normalized value 2
-127 (C) The normalized value 2
-256(D) The normalized value +0
View Answer / Hide AnswerANSWER: The special value +0
(A) 11
(B) 8
(C) 15
(D) 9
View Answer / Hide Answer(49) If p denotes the number system radix then the only value of p that satisfy the equation √121p =
11p is(A) Any value >2
(B) Any value <2
(C) Decimal 10
(D) None of the above
View Answer / Hide Answer(50) The 2’s complement representation of P, which is a 16-bit signed integer, is (F87B)16. What is the 2s ’complement representation of 8*P?(A) (1870)
16(B) (C3D8)
16(C) (ACD8)
16(D) (C103)
16View Answer / Hide Answer(51) The Boolean function (AB+C) is to be implemented using only 2-input NOR gates. The minimum number of gates required is(A) 5
(B) 4
(C) 3
(D) 2
View Answer / Hide Answer(52) How many D flip-flops are needed to design a mod-258 counter?(A) 121
(B) 5
(C) 258
(D) 9
View Answer / Hide Answer